Division euclidienne de polynômes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
psp
- Membre Relatif
- Messages: 312
- Enregistré le: 23 Oct 2007, 14:35
-
 par psp » 27 Nov 2013, 20:44
par psp » 27 Nov 2013, 20:44
Bonsoir,
J'essaie de trouver une méthode permettant de déterminer le reste de la division euclidienne d'un polynôme par un autre.
Ce que mon cours dit :
Soit

et

,

Donc

tel que P = Q.B + R pour deg(R)2000)
-
mr_pyer
- Membre Relatif
- Messages: 137
- Enregistré le: 07 Avr 2013, 20:42
-
 par mr_pyer » 27 Nov 2013, 20:56
par mr_pyer » 27 Nov 2013, 20:56
Une bonne méthode pour trouver le reste c'est de remplacer

par les racines
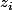
du diviseurs
)
dans l'égalité
=Q(X)B(X)+R(X))
, tu te rerouves alors avec
=R(z_i))
...
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 27 Nov 2013, 21:41
par deltab » 27 Nov 2013, 21:41
Bonsoir.
[quote="psp"]Soit

et

,

Donc

tel que P = Q.B + R pour deg(R)2000.
-
mr_pyer
- Membre Relatif
- Messages: 137
- Enregistré le: 07 Avr 2013, 20:42
-
 par mr_pyer » 27 Nov 2013, 21:53
par mr_pyer » 27 Nov 2013, 21:53
Ce serait plutôt les racines du diviseurs
)
Pour moi le diviseur c'est
)
et pour toi c'est
)
ça revient au même...
P.S. : Désolé pour le double poste je ne sais pas si c'est le forum ou ma connexion...
-
mr_pyer
- Membre Relatif
- Messages: 137
- Enregistré le: 07 Avr 2013, 20:42
-
 par mr_pyer » 27 Nov 2013, 21:57
par mr_pyer » 27 Nov 2013, 21:57
Pour toi
)
c'est le diviseur, pour moi c'est
)
on dit la même chose.
En général

c'est le quotient mais moi ça me gène pas.
-
psp
- Membre Relatif
- Messages: 312
- Enregistré le: 23 Oct 2007, 14:35
-
 par psp » 27 Nov 2013, 22:51
par psp » 27 Nov 2013, 22:51
Ouiiiiii je vais essayer merci beaucoup :))
-
Losange
- Membre Naturel
- Messages: 60
- Enregistré le: 14 Nov 2013, 23:51
-
 par Losange » 27 Nov 2013, 22:58
par Losange » 27 Nov 2013, 22:58
Il y a plus simple : l'algorithme de la division euclidienne sur les entiers s'adapte facilement au calcul sur les polynômes.
Algorithme :
On pose B=0
et R= P
Tant que
\geq deg(Q))
faire :
Trouver le monôme M tel que R et MQ ont le même monôme dominant.
Affecter (B,R)=(B+M,R-MQ).
Fin de "tant que".
Renvoyer B et R.
Exemple :
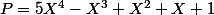
et

Premier passage dans la boucle :


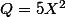
Deuxième passage dans la boucle :
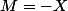

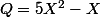
Troisième passage dans la boucle :
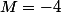

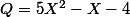
A là fin, on a :
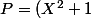 (5X^2-X-4) + (2X+5))
-
mr_pyer
- Membre Relatif
- Messages: 137
- Enregistré le: 07 Avr 2013, 20:42
-
 par mr_pyer » 27 Nov 2013, 23:22
par mr_pyer » 27 Nov 2013, 23:22
Oui, mais par exemple si je te demande le reste de la division euclidienne de
X+\cos(a))^n)
par
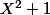
je doute que cette méthode fonctionne. Inutile de s'embêter à calculer le quotient si on demande juste le reste...
-
psp
- Membre Relatif
- Messages: 312
- Enregistré le: 23 Oct 2007, 14:35
-
 par psp » 27 Nov 2013, 23:33
par psp » 27 Nov 2013, 23:33
mr_pyer j'aime bien ta méthode je retombe sur mes pattes avec, (finalement les valeurs qu'avait choisi mon prof étaient les racines du quotient mais il ne l'as pas dit donc merci maintenant je sais)
Par contre as tu un moyen fiable de connaitre le degré de R ?
J'imagine qu'il est fonction du nombres de racines de Q, sachant que si R est de degré 4 il faut un système de 4 lignes (donc Q doit au moins avoir 4 racines) puisque le reste est unique, peux tu confirmer ?
-
mr_pyer
- Membre Relatif
- Messages: 137
- Enregistré le: 07 Avr 2013, 20:42
-
 par mr_pyer » 27 Nov 2013, 23:42
par mr_pyer » 27 Nov 2013, 23:42
C'est bizarre que ton prof n'est pas précisé que l'on teste en prenant les racines de

(j'ai du mal à m'y faire avec

pour le diviseur :mur:), t'es sûr que tu écoutais à ce moment là :lol3: ?
Sinon tu dois savoir que
<\mathrm{deg}(Q))
donc tu le connais le degré.
Pour le nombre d'équation, tu en auras tout juste assez puisque que

à (multiplicité comprise) exactement
)
racines.
Parfois il peut arriver qu'il y ait des racines multiples, dans ce cas il faut dériver l'égalité
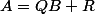
et re-remplacer

par la racine multiple. (j'espère ne pas t'avoir perdu je te donnerai un exemple s'il faut)
-
psp
- Membre Relatif
- Messages: 312
- Enregistré le: 23 Oct 2007, 14:35
-
 par psp » 27 Nov 2013, 23:46
par psp » 27 Nov 2013, 23:46
mr_pyer a écrit:C'est bizarre que ton prof n'est pas précisé que l'on teste en prenant les racines de

(j'ai du mal à m'y faire avec

pour le diviseur :mur:), t'es sûr que tu écoutais à ce moment là :lol3: ?
Sinon tu dois savoir que
<\mathrm{deg}(Q))
donc tu le connais le degré.
Pour le nombre d'équation, tu en auras tout juste assez puisque que

à (multiplicité comprise) exactement
)
racines.
Parfois il peut arriver qu'il y ait des racines multiples, dans ce cas il faut dériver l'égalité
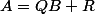
et re-remplacer

par la racine multiple. (j'espère ne pas t'avoir perdu je te donnerai un exemple s'il faut)
Peux tu avec
^{2}})
1 et -1 sont dont racine doubles
Et si j'écoutais mais c'était la fin du cours le prof est allé super vite et puisqu'on a controle de 20 minutes chaque semaine je préfère être au point
-
mr_pyer
- Membre Relatif
- Messages: 137
- Enregistré le: 07 Avr 2013, 20:42
-
 par mr_pyer » 27 Nov 2013, 23:55
par mr_pyer » 27 Nov 2013, 23:55
psp a écrit:Et si j'écoutais mais c'était la fin du cours le prof est allé super vite et puisqu'on a controle de 20 minutes chaque semaine je préfère être au point
Oui ça arrive parfois...
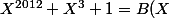\times (X^2-1)^2 + R(X))
(je te laisse écrire les quantificateurs)

doit être de degré inférieur ou égal à 3.
Avec
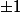
tu as deux équations.
Dérive l'égalité juste au dessus et remplace de nouveau pas
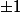
et tu en auras deux autres... (la partie
\times (X^2-1)^2)
on est pas obligé de la dériver puisque ça vaudra

en
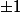
après mais bon).
-
psp
- Membre Relatif
- Messages: 312
- Enregistré le: 23 Oct 2007, 14:35
-
 par psp » 28 Nov 2013, 00:20
par psp » 28 Nov 2013, 00:20
mr_pyer a écrit:Oui ça arrive parfois...
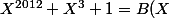\times (X^2-1)^2 + R(X))
(je te laisse écrire les quantificateurs)

doit être de degré inférieur ou égal à 3.
Avec
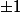
tu as deux équations.
Dérive l'égalité juste au dessus et remplace de nouveau pas
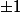
et tu en auras deux autres... (la partie
\times (X^2-1)^2)
on est pas obligé de la dériver puisque ça vaudra

en
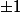
après mais bon).
Donc j'ai :
R(1) = 3
R(-1) = 1
Quand je dérive j'obtiens
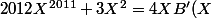(X^{2}-1) + R'(X))
Je trouve trois racines : {

}
R'(0) = 0
R'(1) = 2015
R'(-1) = -2009
Je pose
 = aX^{3} + bX^{2} + cX + d)
 = 3aX^{2} + 2bX + c)
J'ai donc :
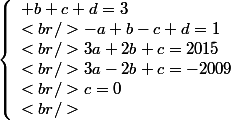
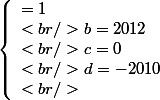
Est ce que je suis à côté de la plaque ?
Si j'ai bien compris deg R <= deg Q - 1
Donc pour l'identification je pose d'abord R de degré (deg(Q) - 1)
-
mr_pyer
- Membre Relatif
- Messages: 137
- Enregistré le: 07 Avr 2013, 20:42
-
 par mr_pyer » 28 Nov 2013, 00:23
par mr_pyer » 28 Nov 2013, 00:23
Ça m'a l'air bien.
Edit : Je te fais confiance pour le système. Pour le 0 tu n'en a pas vraiment besoin puisque tu n'as que 4 inconnues. Mais c'est bien de l'avoir vu ça permet de trouver directement

.
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 28 Nov 2013, 23:27
par deltab » 28 Nov 2013, 23:27
Bonsoir.
mr_pyer a écrit:Pour toi
)
c'est le diviseur, pour moi c'est
)
on dit la même chose.
En général

c'est le quotient mais moi ça me gène pas.
Dans l'énoncé, il y a eu une intervention de notations
Soit

et

,

Donc

tel que P = Q.B + R pour deg(R)<n .
Ici Q(x) est bien le diviseur et B(x) le quotient (le diviseur est supposé connu (ici Q) et on cherche le quotient et le reste (ici B et R).
Autre remarque, si B est supposé connu, on a alors directement R(X)=P(X)-B(X)Q(X), pourquoi chercher les racines de B(X) problème beaucoup plus compliqué que de faire le produit et la différence de 2 polynômes.
-
mr_pyer
- Membre Relatif
- Messages: 137
- Enregistré le: 07 Avr 2013, 20:42
-
 par mr_pyer » 28 Nov 2013, 23:50
par mr_pyer » 28 Nov 2013, 23:50
Oui l'énoncé inverse les notations standard. Je ne l'avais pas vu dans mon premier poste mais je l'avais remarqué depuis.
Autre remarque, si B est supposé connu, on a alors directement R(X)=P(X)-B(X)Q(X), pourquoi chercher les racines de B(X) problème beaucoup plus compliqué que de faire le produit et la différence de 2 polynômes.
Le truc c'est que le quotient (ici noté B) est beacoup plus difficile à obtenir que le reste.
L'exemple que je donne au dessus (avec
 X+\cos(a))^n)
), on calcule le reste en 30 secondes chrono, alors que le quotient... je ne sais même pas s'il est calculable...
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 29 Nov 2013, 01:30
par deltab » 29 Nov 2013, 01:30
Bonjour.
Peut-être via une relation de récurrence.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 29 Nov 2013, 07:48
par Ben314 » 29 Nov 2013, 07:48
Ou en écrivant simplement B=(P-R)/Q...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 29 Nov 2013, 21:59
par deltab » 29 Nov 2013, 21:59
Bonsoir.
Ben314 a écrit:Ou en écrivant simplement B=(P-R)/Q...
Oui, on peut se suffire de cette expression de B, mais trouver l'expression polynomiale de B c'est autre chose bien qu'on sache que P-R est divisible par Q.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 29 Nov 2013, 23:30
par Ben314 » 29 Nov 2013, 23:30
Perso, je disais ça en pensant "trés fort" à

qui est plus court à écrire (et aussi souvent plus simple à manipuler) sous cette forme que sous la forme
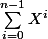
...
Aprés, concernant par exemple la division de
X+\cos(a)\big)^n)
, par
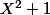
, tu peut remplacer la division par une multiplication par
^k}{X^{2(k+1)}})
et, si tu ne garde dans le produit que les termes en
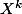
avec

, ça te donne le quotient de la division (les termes en
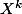
avec
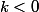
correspondant évidement à
}{X^2+1})
où

est le reste de la division.)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
(j'ai du mal à m'y faire avec
pour le diviseur :mur:), t'es sûr que tu écoutais à ce moment là :lol3: ?
donc tu le connais le degré.
à (multiplicité comprise) exactement
racines.
et re-remplacer
par la racine multiple. (j'espère ne pas t'avoir perdu je te donnerai un exemple s'il faut)
(je te laisse écrire les quantificateurs)
doit être de degré inférieur ou égal à 3.
tu as deux équations.
et tu en auras deux autres... (la partie
on est pas obligé de la dériver puisque ça vaudra
en
après mais bon).
c'est le diviseur, pour moi c'est
on dit la même chose.
c'est le quotient mais moi ça me gène pas.