Divisibilité
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mu4l
- Messages: 7
- Enregistré le: 04 Avr 2012, 20:47
-
par mu4l » 08 Mar 2014, 09:49
Bonjour,
Je bloque sur la question suivante :
Convertissez 656353 en base 16, puis déduisez en que 17 divise
Donc j'ai calculé 656353 en base 16 qui me donne a03e1.
Mais je ne vois pas comment vérifier que 17 divise
Donc si quelqu'un peu me donner un coup de main je l'en remercie.
-
Gonra
- Membre Relatif
- Messages: 100
- Enregistré le: 06 Déc 2012, 21:34
-
par Gonra » 08 Mar 2014, 10:01
Bonjour ,
656353=16*41022+1
et 267^{16} = 1 modulo(17) [petit théorème de Fermat ]
tu remplaces 656353 dans 267^{656353}-12 puis tu fais le calcul modulo 17.
-
mu4l
- Messages: 7
- Enregistré le: 04 Avr 2012, 20:47
-
par mu4l » 08 Mar 2014, 16:24
Bonjour,
Merci de ta réponse, mais je doute sur la réponse, j'ai bien compris les deux premiére lignes,
Mais quand je remplace 656353 dans
je ne suis pas sur de la réponse :
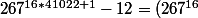^{41022+1}-12 = 1^{41022+1}-12 [17])
Il me semble que j'ai du raté une étape avec les puissance mais je vois pas quel est l'erreur.
-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
par Ben314 » 08 Mar 2014, 17:51
Rappel : ^m=a^{n\times m})
et, selon ma nièce qui est au collège, 16*41022+1, c'est pas égal à 16*(41022+1)... :doh:
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
