Divisibilité dans R[X]
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par matheuxendetresse » 30 Sep 2023, 17:08
par matheuxendetresse » 30 Sep 2023, 17:08
Bonjour,
On a:

On veut prouver que:

Je vois pas comment le faire ni avec la récurrence ni avec la division euclidienne, j'ai essayé mais ça n'a pas marché pour moi.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6133
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 30 Sep 2023, 17:28
par GaBuZoMeu » 30 Sep 2023, 17:28
Bonjour,
Quand je suis à court d'idée pour un problème comme ça, je regarde ce qui se passe pour

, pour

, je réfléchis dessus ... et puis l'idée vient.
 par matheuxendetresse » 30 Sep 2023, 17:45
par matheuxendetresse » 30 Sep 2023, 17:45
GaBuZoMeu a écrit:Bonjour,
Quand je suis à court d'idée pour un problème comme ça, je regarde ce qui se passe pour

, pour

, je réfléchis dessus ... et puis l'idée vient.
Ah oui j'ai réessayé et ça a marché justement avec la division euclidienne, je l'ai faite de

par

, et puis de
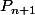
par


Merci
-
GaBuZoMeu
- Habitué(e)
- Messages: 6133
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 01 Oct 2023, 10:09
par GaBuZoMeu » 01 Oct 2023, 10:09
Avec plaisir.
Une fois vu le truc, on peut présenter ainsi :
On constate que
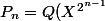)
, où
=Y^2+Y+1)
, dont les deux racines sont

et

. De même
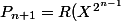)
où
=Y^4+Y^2+1)
dont les quatre racines sont
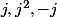
et
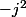
.
 par matheuxendetresse » 01 Oct 2023, 11:47
par matheuxendetresse » 01 Oct 2023, 11:47
GaBuZoMeu a écrit:Avec plaisir.
Une fois vu le truc, on peut présenter ainsi :
On constate que
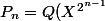)
, où
=Y^2+Y+1)
, dont les deux racines sont

et

. De même
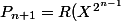)
où
=Y^4+Y^2+1)
dont les quatre racines sont
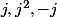
et
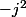
.
Ah oui ça aussi résout le problème, je l'ai pas vu comme ça.
Merci : )
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
, pour
, je réfléchis dessus ... et puis l'idée vient.
, où
, dont les deux racines sont
et
. De même
où
dont les quatre racines sont
et
.