Divisibilité dans Z
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
nix64
- Membre Relatif
- Messages: 109
- Enregistré le: 06 Déc 2018, 10:17
-
 par nix64 » 07 Jan 2019, 10:06
par nix64 » 07 Jan 2019, 10:06
Bonjour
la question est

voila comment j ai pensé

donc j ai fini par trouvé que si n=4k+2 alors
)
est ce que j ai l equivalence ici c à d est ce que je peux dire que
\Leftrightarrow n=4k+2)
,
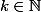
-
aviateur
 par aviateur » 07 Jan 2019, 10:50
par aviateur » 07 Jan 2019, 10:50
Bonjour
Le fait de demander si tu as équivalence c'est que tu n'as surement pas raisonné correctement.
Modulo 7 on a:
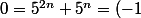^n+5^n)
Si n=2p :
^n+5^n=1+(-1)^p=0)
équivalent à p impair.
donc n=2(2k+1) sont sol.
si n=2p+1
^n+5^n=-1+5 (-1)^p=0)
il faut continuer pour voir si il y a des solutions dans ce cas là.

-
nix64
- Membre Relatif
- Messages: 109
- Enregistré le: 06 Déc 2018, 10:17
-
 par nix64 » 07 Jan 2019, 11:18
par nix64 » 07 Jan 2019, 11:18
est ce que j aurai pu raisonner comme ça

{4k;4k+1;4k+2;4k+3} avec k un entier naturel et je verifie pour chacune des valeurs de n

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 07 Jan 2019, 11:43
par Ben314 » 07 Jan 2019, 11:43
Salut,
Perso, j'aurais commencé par dire que, comme 13 est premier, pour qu'il divise
)
il faut (et il suffit) qu'il divise l'un des deux termes du produit, mais comme il ne peut pas diviser
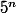
c'est qu'il doit diviser

ce qui signifie qu'on doit avoir

Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
nix64
- Membre Relatif
- Messages: 109
- Enregistré le: 06 Déc 2018, 10:17
-
 par nix64 » 07 Jan 2019, 12:23
par nix64 » 07 Jan 2019, 12:23
Ben314 a écrit:Salut,
Perso, j'aurais commencé par dire que, comme 13 est premier, pour qu'il divise
)
il faut (et il suffit) qu'il divise l'un des deux termes du produit, mais comme il ne peut pas diviser
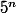
c'est qu'il doit diviser

ce qui signifie qu'on doit avoir

merci c est le lemme de Gauss que vous avez utiliser
maintenant comme

et on a verifié deja que

est ce que on peux dire que n=4k+1
on cherche une condition necessaire et suffisante sur l indice de la puissance

-
nix64
- Membre Relatif
- Messages: 109
- Enregistré le: 06 Déc 2018, 10:17
-
 par nix64 » 07 Jan 2019, 16:18
par nix64 » 07 Jan 2019, 16:18
vous ne m'avez pas répondu s'ils vous plait j ai posé la question est ce que c est correcte d écrire

{4k;4k+1;4k+2;4k+3} avec k un entier naturel
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 07 Jan 2019, 16:37
par pascal16 » 07 Jan 2019, 16:37
pourquoi pas :
N= {4k+p,p€{0;1;2;3}, k€N}
N=(U,k€N) {4k+p,p€{0;1;2;3}} avec le U de union disjointe
-
aviateur
 par aviateur » 07 Jan 2019, 16:40
par aviateur » 07 Jan 2019, 16:40
Rebonjour
Je ne comprends pas ce que tu cherches.
Dans mon premier message il restait à voir si on a des solutions a
-1+5(-1)^p=0 mod (13)
Mais -1+5(-1)^p=4 ou -6. Donc c'est terminé.
Les seules solutions sont de la forme n=4k+2

-
nix64
- Membre Relatif
- Messages: 109
- Enregistré le: 06 Déc 2018, 10:17
-
 par nix64 » 07 Jan 2019, 16:49
par nix64 » 07 Jan 2019, 16:49
merci beaucoup maintenant je vois claire
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités




il faut (et il suffit) qu'il divise l'un des deux termes du produit, mais comme il ne peut pas diviser
c'est qu'il doit diviser
ce qui signifie qu'on doit avoir