Diviseurs et multiples dans un anneau principal

[Ncdk]

Bonsoir,

J'ai un exercice ou je ne sais pas débuter, ni ou je dois aller, c'est très dérangeant, si vous avez des pistes, des explications à me fournir sur la méthode de résolution, je suis preneur.

1) Montrer que dans , les éléments et ont un PGCD mais pas de PPCM.
2) Montrer que dans , les éléments et n'ont pas de PGCD.
3) Soit A un anneau commutatif intègre et a,b des éléments non nuls de A.

• Montrer que a et b ont un PPCM égale à m si et seulement si
• Montrer que dans ce cas,

[Robot]

Tu peux commencer par 3). La première partie est quasiment la définition du ppcm, et la deuxième pas trop compliquée.

[Ncdk]

Pour la a) :

Si j'applique la définition : On dit que est un PPCM de a, b si les multiples communs à a, b sont exactement les multiples de m, c'est-à-dire que et si et seulement si

Donc m' est un multiple de a et m' est un multiple de b si et seulement si m' est un multiple de m.

Je vois pas comment finir, est-ce que m' est une sorte d'ensemble, c'est-à-dire qu'il existe plusieurs m' qui sont multiple de a ?
J'avais l'idée d'intersecter l'ensemble des multiples de a avec l'ensemble des multiples de b pour que ça donne l'ensemble des multiple de m.

Pour la b) :

On peut partir du fait que .
Donc du coup et comme A est intégre, on peut utiliser la "notation"
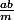
(Donc il existe un tel que ) Est-il unique ?

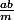
Du coup là, je sais pas quoi faire dans un second temps, il faut montrer que divise a et divise b ?

[Robot]

Je vois pas comment finir, est-ce que m' est une sorte d'ensemble, c'est-à-dire qu'il existe plusieurs m' qui sont multiple de a ?

??????????????????? m' est un élément de A. Qu'est-ce que tu racontes ?
Ne vois-tu pas un rapport entre l'ensemble des multiples de a et l'idéal engendré par a ?

[Ncdk]

??????????????????? m' est un élément de A. Qu'est-ce que tu racontes ?
Ne vois-tu pas un rapport entre l'ensemble des multiples de a et l'idéal engendré par a ?

L'idéal engendré par a c'est l'intersection des ensembles des multiples de a ?

[Robot]

L'idéal engendré par a c'est l'intersection des ensembles des multiples de a ?

:triste:
Peux tu m'expliquer ce que sont "les ensembles des multiples de a" ? Il y en a plusieurs ?
Réfléchis à ce que tu écris !

[Ncdk]

Ce que je voulais dire c'était :

Les multiples de a c'est un ensemble.
Les multiples de b c'est aussi un ensemble.

Du coup leur intersection c'est un ensemble, les multiples de m.

Je le vois comme ça en tout cas.

[Ben314]

Oui, mais c'est encore très mal formulé : l'intersection de l'ensemble des multiples de a et de l'ensemble des multiples de b, c'est évidement un ensemble, mais ce n'est pas forcément l'ensemble des multiple de quelque chose. Si c'est effectivement l'ensemble des multiple d'un certain m, alors a et b ont un ppcm qui est m (mais ce ppcm n'est en général pas unique).

[Robot]

Ncdk, tu ne vois toujours pas quel rapport il y a entre l'ensemble de multiples de a et l'idéal engendré par a ? Si tu ne sais pas répondre correctement à cette question, c'est que tu es bien à côté du sujet ! Revois les définitions.

[Ncdk]

@Ben :

D'accord merci, et comment je peux faire une preuve rigoureuse dans ce cas ?
En appliquant la définition, on a bien que l'ensemble des multiples de a, que l'on note Mul(a) et l'ensemble des multiples b, vérifie : Mul(a) \cap Mul(b) = Mul(m) ?

@Robot :

Non je vois pas, je n'ai pas cette définition en tout cas, ou alors je l'ai mais peut-être pas formulé de cette manière, je sais que pour A un anneau principal, , et . Tout générateur de l'idéal est un PPCM de

[Ben314]

En appliquant la définition, on a bien que l'ensemble des multiples de a, que l'on note Mul(a) et l'ensemble des multiples b, vérifie : Mul(a) \cap Mul(b) = Mul(m) ?

Exprimé comme ça, il te manque toujours la partie la plus importante de la définition, a savoir de déterminer si Mul(a) \cap Mul(b) est ou n'est pas l'ensemble des multiple de quelque chose.
Sinon, comme le dit Robot, il faudrait peut-être au minimum comprendre les définitions qu'il y a dans ton cours : l'ensemble des multiples de A, c'est (par définition) l'idéal engendré par a et ça se note ou bien (a) ou bien aA, mais je ne crois pas avoir déjà vu du Mul(a).
Et concernant l'exo. ben faut (évidement) commencer par regarder que est l'ensemble de multiples communs de a=3 et b=2+i.racine(5) (dans A) pour ensuite voir si c'est l'ensemble des multiple de quelque chose. En utilisant le vocabulaire du cours, ça signifie déterminer l'intersection des idéaux engendrés par a et par b puis regarder si cet idéal est principal ou pas.

[chan79]

salut
A propos de la question 1:
On cherche les diviseurs de 3

En passant aux modules et en élevant au carré:

Il n'est pas possible que les deux facteurs soient égaux à 3.
Au signe près, les seuls diviseurs de sont et
De même, les seuls diviseurs de au signe près sont et
Les diviseurs communs à et sont et .
On peut donc dire que est un PGCD de et .
Pour la question 2, voir et qui sont des diviseurs communs.

[Ncdk]

@Ben :

J'ai beau cherché dans mon cours, j'ai pas cette définition dans mon cours, peut-être vu les années précédentes.

Je pense que tu voulais dire l'ensemble des multiples de a, au passage, et non pas A.

@Chan :

Je vais y réfléchir, je poste de nouveau le résultat plus tard, merci :)

[Ben314]

@Ben :
J'ai beau cherché dans mon cours, j'ai pas cette définition dans mon cours, peut-être vu les années précédentes.

J'ai du mal a imaginer un cours (universitaire) parlant de ppcm et de pgcd où on ne définit pas AVANT ce qu'est un un idéal dans un anneau et ce qu'est l'idéal engendré par ....
Sans parler que dans l'exercice lui même, à la question 3), il y a écrit et ce qui laisse un tout petit peu supposer que l'étudiant a qui on a filé l'exo. est sensé savoir ce que signifie cette notation.

[Ncdk]

J'ai du mal a imaginer un cours (universitaire) parlant de ppcm et de pgcd où on ne définit pas AVANT ce qu'est un un idéal dans un anneau et ce qu'est l'idéal engendré par ....
Sans parler que dans l'exercice lui même, à la question 3), il y a écrit et ce qui laisse un tout petit peu supposer que l'étudiant a qui on a filé l'exo. est sensé savoir ce que signifie cette notation.

Ah oui, je vois je vois, non mais ce que je voulais dire c'est qu'on l'a pas définit comme ça dans mon cours, de plus j'ai pas fait le rapprochement avec la définition d'un idéal dans un anneau et ce qu'est l'idéal engendré par...

Mais c'est vrai que l'ensemble des multiples de a d'un anneau, c'est donc l'idéal engendré par a.
Mais, je comprends pas pourquoi, ça doit pas être compliqué, mais je vois pas en tout cas.
D'ailleurs, on peut définir l'ensemble des diviseur de a d'un anneau ?
Autant que j'ai les deux, je pourrais peut-être avancé

[Ben314]

On peut évidement définir l'ensemble des diviseurs d'un élément a donné d'un anneau A (on vient de le faire....) par contre, je ne crois pas que ça porte de nom particulier a part "ensemble des diviseurs de a".
Il faut dire aussi que ça n'a pas de propriété algébrique aussi remarquable que l'ensemble des multiple de a :
- La somme de deux multiples de a est un multiple de a et le produit d'un multiple de a par n'importe quoi est un multiple de a (en bref, l'ensemble des multiple de a est un idéal...)
- Alors que la somme de deux diviseurs de a n'est en général pas un diviseur de a et, de même, le produit de deux diviseurs de a n'est pas forcément diviseur de a. C'est donc nettement "moins bien structuré" comme ensemble (le seul truc qui me vient à l'esprit comme "structure", c'est qu'un diviseur d'un diviseur de a est lui même diviseur de a)