Diviseur

[titi0072]

:marteau: bonjour,j'aimerai savoir si ma 1ère reponse est juste et si on pourrait m'aider pour le reste, j'arrive pas.merci d'avance :triste:

[COLOR=Red][COLOR=Teal]Soit n un entier positif et p un entier plus grand que 2.
a)montrer que pgcd((p^n)+1,p)=1
En déduire pgcd((p^2n)-1, p^(n+1)-p).
b)montrer que pgcd(p^n, sigma p^k (avec k=0 et allant jusqu'a (n-1))).
En déduire pgcd(p^n-1, p^(n+1)-p^n).[/COLOR][/COLOR]

=>Preuve:pour montrer que pgcd((p^n)+1,p)=1
considérons le nmbre A=p*p*...p +1 avec p*p..*p=p^n
alors p*p*..*p est le facteur de n fois le nombre p donc p divise p*p..*p
donc p divise 1=A-p^n.Mais cela est impossible car les dseuls diviseurs de 1 sont 1 et -1 et l'on a p>2. donc p^n+1 et p sont premier entre eux
est'ce correct?

[alben]

bonjour,

je ne pense pas que ta preuve soit correcte, tu as juste montré que p ne divisait pas A. Il te faudrait faire le même raisonnement avec un diviseur de p au lieu de p.
De manière plus élégante tu peux utiliser Bezout Au+pv=1 avec u=1 et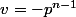
pour la suite utilise le fait que (p^2n)-1=(p^n)²-1=identité remarquable

[titi0072]

j'ai besoin d'aide pour la question b) svp je n'arrive vraiment pas...