Diviseur commun
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
hamdo
- Membre Naturel
- Messages: 59
- Enregistré le: 24 Avr 2008, 21:13
-
 par hamdo » 10 Mai 2008, 11:34
par hamdo » 10 Mai 2008, 11:34
Salut les Matheux
soient
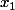
;
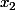
;... et

des entiers relatifs
Pourquoi
 \Longleftrightarrow240/ (x_{1}^{5}+x_{2}^{5}+...+x_{n}^{5}))
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 10 Mai 2008, 11:45
par Quidam » 10 Mai 2008, 11:45
hamdo a écrit:Salut les Matheux
soient
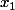
;
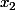
;... et

des entiers relatifs
Pourquoi
 \Longleftrightarrow240/ (x_{1}^{5}+x_{2}^{5}+...+x_{n}^{5}))
Le signe

s'emploie pour indiquer l'équivalence de deux affirmations.
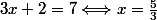

est une affirmation
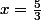
est une autre affirmation
Dire
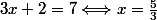
c'est affirmer que si

alors
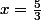
et que si
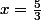
alors

Par conséquent dire :
 \Longleftrightarrow240/ (x_{1}^{5}+x_{2}^{5}+...+x_{n}^{5}))
c'est affirmer que si
)
alors
)
et que si
)
alors
)
Comme
)
n'est pas une affirmation, et que
)
n'en est pas une non plus,
 \Longleftrightarrow240/ (x_{1}^{5}+x_{2}^{5}+...+x_{n}^{5}))
n'a aucun sens !
Et demander pourquoi
 \Longleftrightarrow240/ (x_{1}^{5}+x_{2}^{5}+...+x_{n}^{5}))
n'a aucun sens non plus !
-
hamdo
- Membre Naturel
- Messages: 59
- Enregistré le: 24 Avr 2008, 21:13
-
 par hamdo » 10 Mai 2008, 11:59
par hamdo » 10 Mai 2008, 11:59
Salut Quidam
a et b étant deux entiers relatifs.
a/b signifie que a divise b c-à-d b=ka avec k entier relatif
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 10 Mai 2008, 12:01
par Quidam » 10 Mai 2008, 12:01
hamdo a écrit:Salut Quidam
a et b étant deux entiers relatifs.
a/b signifie que a divise b c-à-d b=ka avec k entier relatif
OK, je l'ignorais ! Moi j'aurais écrit a|b, mais bon ...
Dans ce cas, je n'ai rien dit !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités
;
;... et
des entiers relatifs