Distributions

[bou3ou]

bonjour,

voila je passe un ratrappage en une matiere que je trouve assez compliqué j'ai besoin des solutions de l'examen que j'ai passé a la premiere session pour avoir une chance de la valider ou du moins limiter la casse si vous pouvez m'aider a resoudre cet exercice je vous en serai reconnaissant

1; trouver toute les distributions u dans D'(R) telles que

u"(x)+u'(x)-6u(x)= m(x)
ou m(x) est la masse de dirac concentrée en 0

2 trouver les solutions u dans S'(x) satisfaisant l'equation
3 trouver toutes les solutions u dans D'(x) satisfaisant l'equation et u dnas L^2(R)


merci pour votre aide

[mathelot]

Salut,

quelques explications sur la théorie des distributions (vite fait)

ça a été inventé par laurent Schwartz il y a une trentaine d'années.

A la base (c'était avant les espaces de Sobolev), c'est un procédé qui
perme de dériver des fonction..non dérivables.

l'idée , pour une fonction très pathologique, que l'on souhaite dériver, est de la multiplier par une fonction , elle, extrememnt régulière,ie, de classe à support compact

et pour dériver la fonction f, de faire jouer la dualité issue de la bilinéarité
du produit (une sorte de produit scalaire , si tu veux)
et par intégration par parties, de dériver au lieu de

d'après la formule de Green, ce procédé marche bien mais induit un phénomène de "bord"

exemple:




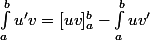
le terme de bord est qui vient gêner la dérivation
, en compliquant les dérivations ultérieures
c'est le souci, par exemple, des nombreux termes de bord
des formules de Taylor avec reste intégral.


Pour cette raison , l'on teste sur des fonctions
dont le support est à l'intérieur du domain, donc
des termes de bord nuls.


Pour tes équa diff, tu "cognes" les fonctions (en fait un produit tout simple)
avec une fonction à support compact ,
par dualité tu transposes la dérivation sur
et non plus sur u,et la forme linéaire obtenue est dite "solution de l'équa diff".

[Arkhnor]

Bonjour.

(c'était avant les espaces de Sobolev),

Les travaux de Sobolev sont antérieurs à ceux de Schwartz, tout comme ceux de Gelfand. Quant à savoir à qui revient la paternité des distributions, c'est un vieux débat qu'il ne vaut mieux pas ré-ouvrir.
L'apport des distributions à surtout été d'inclure tout ça dans un cadre beaucoup plus général, et de donner un cadre favorable pour la transformée de Fourier.

Pour revenir à l'exercice, la méthode est la même que pour les équations différentielles classiques : on résout d'abord l'équation homogène , ce qui est standard. (les solutions au sens des distributions sont les mêmes qu'au sens classique), on trouve ensuite une solution particulière, et on superpose.

Une fois trouvé toutes les solutions dans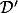 , on regarde quelles sont celles qui appartiennent à et quelles sont celles qui sont des fonctions de .