re-bonjour,
quand j'ai écrit les posts précédents, je pensais que la formule à démontrer était fausse ou incomplète,
et j'ai essayé de la reconstituer. Depuis, j'ai changé d'avis (la formule à démontrer est vraie) et j'ai regardé un peu le cours sur les séries de Fourier.
Comme autre démonstration , il suffit de montrer que
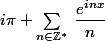
est la série de Fourier de la fonction

périodique f
dont la restriction à l'intervalle
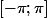
est
)
avec
=0)
pour x<0
=\frac{1}{2})
=1)
pour x >0
Calculons les coefficients de Fourier de f:
e^{-inx}dx =\int_{0}^{\pi} e^{-inx}dx)
e^{-inx}dx =\frac{1}{ni} \left[ e^{-inx}\right]_{\pi}^{0})
e^{-inx}dx =\frac{-i}{n} \left( 1-(-1)^n \right))
après calculs:
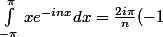^n)
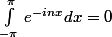
d'où les coefficients de la série trigonométrique valent:
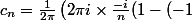^n)+\frac{2\pi}{n} (-1)^n \right))
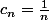
de plus
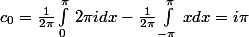
d'où
La fonction f étant de classe C1 par morceaux, elle est somme de sa série de Fourier,
et
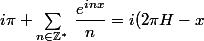)
pour
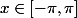
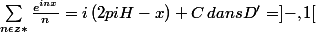
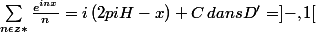
? (Heaviside ?)