Dimension

[titi1]

bonjour,
je cherche la dimension de l'ensemble suivant {P € R3[x] / P(0)=0}
j'ai raisonné de la façon suivante : P s'écrit sous la forme P(x) = a+bX+cX²+dX^3 où a,b,c,d sont des réels non nuls
si P(0) = 0 alors a =0 donc ce ne peut être que le polynome nul?
je ne suis pas sur de ce que j'ai fait et quelle est la dimension du polynome nul?
merci d'avance

[tize]

Bonjour,
considère la forme linéaire qui à P associe P(0).
L'espace que tu recherche n'est rien d'autre que de plus , donc ....

[nuage]

Salut,
je crois qu'il y a des polynômes non nuls qui s'annulent en zéro.
Tu trouve a=0 on peut en conclure que
P(x) = a+bX+cX²+dX^3 = bX+cX²+dX^3

[titi1]

en utilisant la forme linéaire ai-je le droit d'utiliser la formule du rang qui me donnerait : dim (R3[x]) = dim R - dim ker(e0) ---> dim ker(e0)= 4-1=3?
Car je crois que la formule du rang n'est applicable qu'en dimension finie et R3[x] n'est pas de dimension finie... que faire?

[tize]

... R3[x] n'est pas de dimension finie... que faire?

A bon ?!
Sinon nuage t'a indiqué une méthode beaucoup plus simple donc élégante (à mon avis)

[titi1]

je ne vois pas comment résoudre le problème avec l'explication de nuage...
de plus, je voudrais savoir si la formule du rang est applicable?

[tize]

Oui elle l'est. Tu sais au moins quelle est la dimension de ?
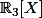
Sinon pour la méthode de Nuage, il t'a dit que les polynômes que tu cherches sont de la forme : bX+cX²+dX^3.
Cela veut dire que est une base de l'espace que tu recherches