Dimension du noyau d un endomorphisme

[nix386]

bonjour
M une matrice carré d ordre n a t on toujours
dim (ker (M) ) = n - rang(M)
si non quand est ce que on peut dire cela

application
M=

peut on dire que rang M = 1 donc dim ker M = 2 donc 0 est une valeur propre d ordre 2
tr (M) = 3
donc le spectre de M est {0,3}
peut t on dire donc que le polynôme caractéristique de M est X²(X-3)
le polynôme minimal est aussi X²(X-3)
puisque dim kerM = 2
donc M est diagonalisable

[Arnaud-29-31]

Salut,

Ca me va jusqu'au moment où tu parles du polynôme minimal.

Et il faudrait peut-être rajouter une toute petite ligne avant de parler du spectre (pour montrer que l'on a bien conscience que lorsque l'on se place dans un corps qui n'est pas algébriquement clos, il faut montrer que M est trigonalisable avant d'écrire somme des vp = trace)

[nix386]

regardons svp la cas de la matrice M

le polynôme caractéristiques de M est X^3
rang(M )= 2 donc dim kerM = 1
donc le polynôme minimal de M est X ?? je ne comprends pas

[nix386]

regardons svp le cas de cette matrice




le polynôme caractéristique de cette matrice est X^3
rg (M)=2 donc dim kerM =1 (3-2)
donc le polynôme caractéristique de M est X ???! je ne comprends
la multiplicité de la valeur propre 0 c est bien dim ker[M-0I] = 1
c est quoi l erreur ?

[Arnaud-29-31]

Le rang c'est bien 2, donc la dimension du noyau c'est bien 1.
Le polynôme caractéristique c'est
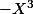
La multiplicité de la valeur propre 0, ce n'est pas dim(ker[M-0.I]) ... ca c'est la dimension du sous espace propre associé à la valeur 0 !
La multiplicité d'une vp, c'est sa multiplicité en tant que racine du polynôme caractéristique.

[nix386]

Le rang c'est bien 2, donc la dimension du noyau c'est bien 1.
Le polynôme caractéristique c'est
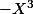
La multiplicité de la valeur propre 0, ce n'est pas dim(ker[M-0.I]) ... ca c'est la dimension du sous espace propre associé à la valeur 0 !
La multiplicité d'une vp, c'est sa multiplicité en tant que racine du polynôme caractéristique.

c est quoi le polynome minimal de M
comment le trouver juste en utilisant la dimension de sous espace propre associé a la valeur propre 0 c est a dire sans calculer M²

[Arnaud-29-31]

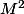
Quand on a affaire à une matrice qui n'est pas diagonalisable, on ne peut pas pondre le polynôme minimal comme ça, il faut en général tester voir si ca marche ... C'est à dire ici on va calculer ... ca donne pas 0 donc le polynôme minimal c'est

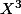
[nix386]

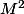
Quand on a affaire à une matrice qui n'est pas diagonalisable, on ne peut pas pondre le polynôme minimal comme ça, il faut en général tester voir si ca marche ... C'est à dire ici on va calculer ... ca donne pas 0 donc le polynôme minimal c'est

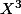
donc ya pas un théorème qui donne le polynôme minimal a partir du polynome caractéristique a partir de la dimension des sous espace propre associé aux valeurs propres ?

regarde dans cette exemple la matrice est diagonalisable semblable a la matrice nulle

[Arnaud-29-31]

Attention, la seule matrice semblable à la matrice nulle est ... la matrice nulle.

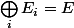
Il y'a bien un théorème qui nous donne le polynôme minimal mais seulement dans le cas où la matrice est diagonalisable (autrement dit si ou encore si la dimension de chaque espace propre est égale à la multiplicité de la vp associée). Ce théorème nous dit que le polynôme minimal n'a que des racines simples.

Autrement dit si tu trouves par un exemple pour une matrice 3x3, un polynôme caractéristique qui est mais que tu as montré que la matrice était diagonalisable (en montrant que ) alors tu peux affirmer que le polynôme minimal est .

[nix386]

donc dans cet exemple le polynôme caractéristique est X²(X-3) la matrice est diagonalisable "car dimker(M)=2"
donc son polynome minimal est X(X-3) pas X²(X-3)

[Arnaud-29-31]

Oui :)
Attention par contre à ne pas oublier le signe - du polynôme caractéristique.

[nix386]

merci beaucoup j avais un gros nuage noir dans la tête :s
je comprends tout maintenant

[Arnaud-29-31]

De rien,

Bonne soirée !