Différentielle totale (début)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
nico2b
- Membre Relatif
- Messages: 271
- Enregistré le: 16 Jan 2007, 17:33
-
 par nico2b » 20 Mai 2007, 15:49
par nico2b » 20 Mai 2007, 15:49
Bonjour, j'aimerai savoir si ma méthode est correct.
Voici l'énnoncé :
Soit f :
 \rightarrow x_1^2 - x_2^2.)
Calculez la dérivée totale de f au point (1,1)
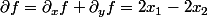
Donc
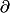
f(1,1) = 0
Calculez la Jacobienne }) au point (1,1).
au point (1,1).
}{(x,y)})
= (

-
 |_{(x,y) = (1,1)})
= ( 2 -2).
Merci pour l'aide apporté...
-
Daniel-Jackson
- Membre Relatif
- Messages: 160
- Enregistré le: 19 Mai 2007, 17:49
-
 par Daniel-Jackson » 20 Mai 2007, 15:56
par Daniel-Jackson » 20 Mai 2007, 15:56
Qu'est ce que tu entend par dérivée totale ? Si c'est la différentiel au point
(1, 1), pour moi la différentielle en un point est donnée par la jacobienne . La différentielle est une application linéaire . Dans le cas présent ce sera une forme linéaire de
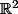
dans

.
Pour moi tu as déjà répondu à la question .
-
Daniel-Jackson
- Membre Relatif
- Messages: 160
- Enregistré le: 19 Mai 2007, 17:49
-
 par Daniel-Jackson » 20 Mai 2007, 15:58
par Daniel-Jackson » 20 Mai 2007, 15:58
nico2b a écrit:Bonjour, j'aimerai savoir si ma méthode est correct.
Voici l'énnoncé :
Soit f :
 \rightarrow x_1^2 - x_2^2.)
Calculez la dérivée totale de f au point (1,1)
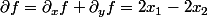
Donc
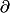
f(1,1) = 0
Désolé moi je ne connaissais pas cette formule et je ne vois pas quelle interpretaion tu donne en additionant les deux dérivée partielles .
-
nico2b
- Membre Relatif
- Messages: 271
- Enregistré le: 16 Jan 2007, 17:33
-
 par nico2b » 20 Mai 2007, 16:07
par nico2b » 20 Mai 2007, 16:07
C'est pcq dans la section différentielle totale du cours, on ne donne pas vraiment de définition clair de la dérivée total, on nous à parlé de la dérivée directionnelle; dérivée partielle kième, dérivée au sens de Gateau et au sens de Fréchet pour finir par la matrice jacobienne.
J'ai donc pensé qu'il fallait additionner les dérivées par rapport à chaque variable.
Et donc pour calculer la dérivée total au point (1,1) je prend la matrice jacobienne (2 -2) que je multiplie par la matrice colone des inconnues on obitent ainsi 2x - 2y d'où mon 0.
-
Daniel-Jackson
- Membre Relatif
- Messages: 160
- Enregistré le: 19 Mai 2007, 17:49
-
 par Daniel-Jackson » 20 Mai 2007, 16:16
par Daniel-Jackson » 20 Mai 2007, 16:16
nico2b a écrit:C'est pcq dans la section différentielle totale du cours, on ne donne pas vraiment de définition clair de la dérivée total, on nous à parlé de la dérivée directionnelle; dérivée partielle kième, dérivée au sens de Gateau et au sens de Fréchet pour finir par la matrice jacobienne.
J'ai donc pensé qu'il fallait additionner les dérivées par rapport à chaque variable.
Et donc pour calculer la dérivée total au point (1,1) je prend la matrice jacobienne (2 -2) que je multiplie par la matrice colone des inconnues on obitent ainsi 2x - 2y d'où mon 0.
Non une fois avoir écrit la matrice c'est fini. En fait la jacobienne est une représentation matricielle de la dérivée totale ( qui à mon avis doit être simplement la différentielle).
Parce que la dérivée en un point c'est la différentielle donc une application linéaire et pour manipuler tout ça on préfère utiliser des matrices puis qu'on est en dimension finie .
Donc il n'ya pas de 0 ni de x ni de y puisque c'est une application . Maintenant oui si tu veux appliquer a un vecteur h de coordonées (x, y) , là oui tu feras le produit matriciel .
Mais une parenthèse juste pour dire que le but du calcul différentiel en général est d'approximer localement les applications pas faciles à controler par des applications linéaires , qui elles sont moins casse pied à étudier .
-
nico2b
- Membre Relatif
- Messages: 271
- Enregistré le: 16 Jan 2007, 17:33
-
 par nico2b » 20 Mai 2007, 16:20
par nico2b » 20 Mai 2007, 16:20
Ok j'ai compris. Merci beaucoup pour cette explication
-
nico2b
- Membre Relatif
- Messages: 271
- Enregistré le: 16 Jan 2007, 17:33
-
 par nico2b » 20 Mai 2007, 19:52
par nico2b » 20 Mai 2007, 19:52
Un autre énoncé dit ceci :
Soit f :
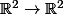
la fonction définie par f(x,y) = ((
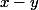^2)
, x+4xy).
Calculez la matrice Jacobienne}) au point (1,1)
au point (1,1)
Pour ça j'ai trouvé la matrice
)
.
Donnez 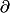 f(1,1)(h) où h
f(1,1)(h) où h  est le vecteur unitaire faisant un angle de 45° avec l'axe des x.
est le vecteur unitaire faisant un angle de 45° avec l'axe des x.
Sur celui-ci je bloque... Quelqu'un aurait-il une piste pour me lancer?
Merci pour votre aide
-
Daniel-Jackson
- Membre Relatif
- Messages: 160
- Enregistré le: 19 Mai 2007, 17:49
-
 par Daniel-Jackson » 20 Mai 2007, 21:00
par Daniel-Jackson » 20 Mai 2007, 21:00
nico2b a écrit:Un autre énoncé dit ceci :
Soit f :
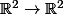
la fonction définie par f(x,y) = ((
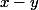^2)
, x+4xy).
Calculez la matrice Jacobienne}) au point (1,1)
au point (1,1)
Pour ça j'ai trouvé la matrice
)
.
Donnez 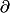 f(1,1)(h) où h
f(1,1)(h) où h  est le vecteur unitaire faisant un angle de 45° avec l'axe des x.
est le vecteur unitaire faisant un angle de 45° avec l'axe des x.
Sur celui-ci je bloque... Quelqu'un aurait-il une piste pour me lancer?
Merci pour votre aide
S'il faiit un angle de 45° c'est qu'il est sur la droite y=x , donc ton vecteur h a pour coordonnée ( x, x) (l'ordonnée est égale à l'abscisse ) .
Et tu fais le produit matriciel de la jacobienne par le vecter (x,x) .
-
nico2b
- Membre Relatif
- Messages: 271
- Enregistré le: 16 Jan 2007, 17:33
-
 par nico2b » 20 Mai 2007, 21:51
par nico2b » 20 Mai 2007, 21:51
Ah daccord merci beaucoup
-
Daniel-Jackson
- Membre Relatif
- Messages: 160
- Enregistré le: 19 Mai 2007, 17:49
-
 par Daniel-Jackson » 20 Mai 2007, 22:31
par Daniel-Jackson » 20 Mai 2007, 22:31
nico2b a écrit:Ah daccord merci beaucoup
Oh pardon j'avais pas vu que h était unitaire , h est alors précisément
le vecteur de coordonnées
)
-
nico2b
- Membre Relatif
- Messages: 271
- Enregistré le: 16 Jan 2007, 17:33
-
 par nico2b » 21 Mai 2007, 15:21
par nico2b » 21 Mai 2007, 15:21
Ce n'est rien merci de me l'avoir signalé
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
la fonction définie par f(x,y) = ((
, x+4xy).
au point (1,1)
.
f(1,1)(h) où h
est le vecteur unitaire faisant un angle de 45° avec l'axe des x.