Différentielle de plusieurs variables DEPENDANTES

[alex769]

bonjour,

cela fait maintenant plusieurs fois que je me pose la même question sans vraiment trouver de réponses satisfaisantes ni sur le net, ni dans les bouquins en ma possession.

Voici donc mon problème:

pourquoi dans la plupart des bouquins est-il précisé dans la présentation des différentielles que les variables de la fonction f(x,y) sont indépendantes? En effet le calcul est exactement le même, si les variables sont dépendantes!!! (df=d_rond_f/d_rond_x . dx + d_rond_f/d_rond_y . dy)

peut être ai-je tord en croyant que le calcul est le même mais le cours de Cauchy (http://visualiseur.bnf.fr/Visualiseur?Destination=Gallica&O=NUMM-90196 ) semble me donner raison.

En fait si vous aviez une explication et des liens vers des publications ou des bouquins pouvant me montrer la subtilité entre la différentielle d'une fonction aux variables indépendantes et la différentielle d'une fonction aux variables dépendantes, j'en serai ravi.

Merci pour tout,

Alexandre

[arnaud32]

comment fais tu pour
f(x,y)=x avec x et y lies par x=y ?

par definition de la differentiel tu as
f(x+h,y+k) = f(x,y) + +o(||(h,k)||)
tu n'as alors pas de direction privilegiee h et k sont 'quelconques'

[alex769]

comment fais tu pour
f(x,y)=x avec x et y lies par x=y ?

par definition de la differentiel tu as
f(x+h,y+k) = f(x,y) + +o(||(h,k)||)
tu n'as alors pas de direction privilégiée h et k sont 'quelconques'

je n'avais pas encore vu cette définition de la différentielle mais en ce qui me concerne j'obtiendrai la chose suivante et ceci quelque soit ma méthode:

méthode 1: je sais qu'il n'y a qu'une seule variable indépendante car x=y => f(x,y)=g(x)
=>df(x,y)=dg(x)=dx

méthode 2: j'applique bêtement la définition donnée dans mon premier post: df(x,y)=1.dx+0.dy=dx


là encore je suis en fait surpris de voir que j'obtiens les mêmes résultats alors que pour la méthode 2 mes variables sont dépendantes.


Mais peut être que cette histoire de direction privilégiée est une piste que je devrais suivre. Pour information dans quel cours as tu trouvé cette définition?

[arnaud32]

mais pourquoi pas faire f(x,y)= que je derive par rapport a x ca me donne 0 et f(x,y)=x que je derive par rapport a y et ca me donne 0 donc
Df = 0 ?

[arnaud32]

la notion de differentielle n'a de sens qu'au voisinage d'un point.
si tu lies x et y, tu privilegies des directions voire tu ne te trouves plus que sur une ligne. ce n'est pas la meme chose.

http://fr.wikipedia.org/wiki/D%C3%A9riv%C3%A9e_directionnelle

[Skullkid]

Bonjour, il s'agit de l'éternel problème du calcul différentiel : le formalisme rigoureux y est lourd (et a d'ailleurs été développé bien après que les gens ont commencé à utiliser le calcul différentiel) donc dès qu'on se place dans un cadre "appliqué" (physique, économie, ...), on fait très vite appel à tout un tas de conventions qui simplifient grandement l'écriture mais rendent parfois floues les définitions et nécessitent de faire appel en retour à des notions du genre "variables indépendantes" ou "variables explicites".

On pourrait disserter assez longuement sur ce qu'est "vraiment" une différentielle en maths et pourquoi, mathématiquement parlant, ça n'a aucun sens de parler de variables dépendantes ou indépendantes. Mais pour abréger et garder les notations "à la physicienne", oui, la formule df = df/dx*dx + df/dy*dy marche aussi si les variables sont dépendantes. Si par exemple dans ton problème x et y sont liés par y = g(x), alors df = df/dx*dx + df/dy*dg/dx*dx. C'est bien la même formule sauf que tu t'astreins à te déplacer selon une certaine direction de ton espace de coordonnées, donnée par dy = dg/dx*dx, c'est pourquoi il serait plus correct de parler de dérivée directionnelle plutôt que de différentielle.

[alex769]

pour ton second post je me suis déjà posé la question moi aussi et la seule explication que j'y vois est que tu ne différencie plus exactement la même fonction car tu la "modifies" en cours de route.

Ensuite , concernant ton dernier post, il ne me semble pas faux de considérer que d'être sur une ligne correspond à être au voisinage d'un point. Mais peut être ai-je là aussi tord.

J'en profite ici pour expliquer le pourquoi de ce sujet:
En physique, lors d'un mélange de 2 gaz, on peut considérer que les propriétés physiques du mélange sont fonctions des variables suivantes:
P,T,m1(masse du composant1) m2 (masse du composant2)
On peut aussi dire que ces mêmes propriétés sont fonctions de:
P, T, Y1 (=m1/(m1+m2)), Y2 (=m2/(m1+m2))
Cependant le lot de variables donné dans la deuxième formulation fait clairement apparaître des variables dépendantes car Y1+Y2=1.

Lors de l'écriture de la différentielle de la fonction h(P,T,Y1,Y2) on voit apparaître la dérivée ronde de h par rapport à Y1 et ceci à P,T et Y2 constant.

Cependant si Y2 est constant, alors Y1 est constant et par conséquent la dérivée de la fonction devrait être nulle (ce que tu semblais plus ou moins suggérer dans ton 2ème post).

Chose surprenante (pour moi), si je ne m'occupe pas de la relation entre Y1 et Y2 et réalise la différentielle de h(P,T,Y1,Y2) comme dans la méthode 2 de mon précédent post, j'obtiens bien les mêmes résultats qu'en réorganisant mon équation h pour ne faire apparaître que (P,T,Y1) par exemple et en calculant la différentielle suivant mes 3 variables indépendantes actuelles que sont P,T et Y1.

J'attends vos lumières avec impatience.

[alex769]

Bonjour, il s'agit de l'éternel problème du calcul différentiel : le formalisme rigoureux y est lourd (et a d'ailleurs été développé bien après que les gens ont commencé à utiliser le calcul différentiel) donc dès qu'on se place dans un cadre "appliqué" (physique, économie, ...), on fait très vite appel à tout un tas de conventions qui simplifient grandement l'écriture mais rendent parfois floues les définitions et nécessitent de faire appel en retour à des notions du genre "variables indépendantes" ou "variables explicites".

On pourrait disserter assez longuement sur ce qu'est "vraiment" une différentielle en maths et pourquoi, mathématiquement parlant, ça n'a aucun sens de parler de variables dépendantes ou indépendantes. Mais pour abréger et garder les notations "à la physicienne", oui, la formule df = df/dx*dx + df/dy*dy marche aussi si les variables sont dépendantes. Si par exemple dans ton problème x et y sont liés par y = g(x), alors df = df/dx*dx + df/dy*dg/dx*dx. C'est bien la même formule sauf que tu t'astreins à te déplacer selon une certaine direction de ton espace de coordonnées, donnée par dy = dg/dx*dx, c'est pourquoi il serait plus correct de parler de dérivée directionnelle plutôt que de différentielle.

Merci pour ta réponse Skullkid.
Aurais-tu un livre à me conseiller sur le calcul différentiel qui expliquerait bien plus en détail ce que tu viens de décrire. En effet, même si je comprends l'idée, ma question sur les dérivées partielles à Y1 constant reste pour moi un mystère qui mérite surement une compréhension plus approfondie de ce à quoi correspond réellement la dérivée partielle.

De même, ces histoires de variables dépendantes ou non e leur application dans le calcul différentiel reste assez flou pour moi, et je ne vois pas l'intérêt de mentionner ce détail lors de la présentation du calcul différentiel.

[Skullkid]

Je n'ai pas de bouquin en tête mais normalement n'importe quel cours de maths sur le calcul diff (pas de "maths pour la physique" ou autres, ceux-là utilisent directement le formalisme simplifié) fournit la "vraie" définition des différentielles. Cela dit il faut un certain bagage en algèbre, et si on se limite aux calculs appliqués, la vraie définition n'est pas utile (elle risque d'ailleurs de t'embrouiller plus qu'autre chose...).

Pour ce qui est de ton problème physique, je pense que ton incompréhension est liée aux subtiles différences de langage entre les maths et la physique. Quand un physicien écrit "f(x,y) = x+2y" il veut dire "la grandeur physique f dépend des grandeurs physiques x et y comme suit". Quand un matheux écrit "f(x,y) = x+2y" il veut dire "je définis une fonction f à deux variables et je donne la recette pour calculer l'image de tous les couples (x,y)".

Tout va bien jusqu'à ce qu'on fasse un changement de variable. Si tu demandes "je pose u = x+y et v = x-y, combien vaut f(u,v) ?", le matheux va te répondre "peu importe comment j'appelle mes variables, f est une fonction qui est ce qu'elle est, donc f(u,v) = u+2v" mais le physicien va te répondre "u et v sont de nouvelles grandeurs physiques dont dépend la grandeur physique f, cette dépendance s'écrit f(u,v) = (3u-v)/2". Le physicien ne voit que des grandeurs qui varient et qui dépendent les unes des autres (des variables et des images) alors que le matheux ne voit que les dépendances elles-mêmes (des fonctions). Là où le drame se joue c'est qu'il faut jongler en permanence avec ces deux points de vue. Et bien sûr, le matheux distingue le nombre f(x) et la fonction f, alors que le physicien écrira indifféremment l'un ou l'autre puisqu'il ne voit qu'un nombre f "qui dépend de x".

Dans ton exemple du mélange gazeux dont les composants ont des masses m1 et m2, admettons que tu t'intéresses à la quantité mu = m1*m2/(m1+m2)^2 = Y1*Y2. Ton système physique vérifiera toujours Y1+Y2 = 1, mais la fonction (Y1,Y2) -> Y1*Y2 elle est ce qu'elle est, elle n'a que faire du sens que tu veux donner à Y1 et Y2, sa différentielle et ses dérivées partielles non plus. Les maths te disent : pour calculer la différentielle de f, tu regardes ses dérivées partielles que tu obtiens en faisant varier un seul paramètre et en fixant les autres. Ces dérivées partielles sont celles de la fonction (l'objet mathématique) et ne correspondent pas forcément à une réalité physique (il est parfois impossible de faire varier un paramètre sans toucher aux autres).

Un autre exemple qui illustre à mon avis assez bien le problème : on considère une particule chargée qui se balade sur un axe et on note sa position x(t). On la suppose de plus soumise uniquement à un champ électrique E(x,t) = E0*cos(kx - omega*t). Avec la seconde loi de Newton tu peux facilement calculer x(t). En physique, on va faire la différence entre et 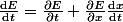. La première formule désigne la variation du champ électrique en fonction du temps ressentie par ta particule si jamais elle restait immobile (ce qui est physiquement impossible puisqu'elle est chargée et qu'on suppose qu'elle est soumise à un champ électrique et rien d'autre) alors que la deuxième formule désigne la variation du champ électrique en fonction du temps physiquement ressentie par ta particule, qui se déplace. Remarque que la notation 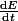n'a pas vraiment de sens du point de vue matheux puisqu'elle sous-entend que E est une fonction d'une seule variable alors qu'on l'a définie comme une fonction de deux variables.

[Dlzlogic]

Bonsoir Skulkid,
Ta longue explication suscite quelque étonnement voire quelques interrogations. Je citerai juste ceci :

Pour ce qui est de ton problème physique, je pense que ton incompréhension est liée aux subtiles différences de langage entre les maths et la physique. Quand un physicien écrit "f(x,y) = x+2y" il veut dire "la grandeur physique f dépend des grandeurs physiques x et y comme suit". Quand un matheux écrit "f(x,y) = x+2y" il veut dire "je définis une fonction f à deux variables et je donne la recette pour calculer l'image de tous les couples (x,y)".

Je suis sûr que tu as soigneusement posé tes mots.
Quand j'étais au stade de l'apprentissage, on avait plutôt tendance à regretter que nos connaissance en mathématique étaient insuffisantes par rapport à ce dont on avait besoin en physique.
Maintenant la tendance serait plutôt de dire que ces deux notions n'ont pas grand rapport et telle chose a tel sens en mathématique, et pas le même en physique, science du réel par excellence.
Bonne soirée.

[ffpower]

Bah c'est juste la forme qui change, mais le fond est le même..

Et en réalité, même en maths, la notation "physique" reste utilisée pour les changements de coordonnées (en géométrie surtout), utiles pour ne pas se noyer dans les notations (même si ces notations continuent à me perturber perso)..

Fin donc ne t'inquiète pas, les maths et la physique continuent à être intrèsèquement liés :we:

[Skullkid]

Comme ffpower le dit, c'est une histoire de notations et je n'ai utilisé la distinction entre "le matheux" et "le physicien" qu'à titre indicatif, en vrai tout le monde mélange les deux formalismes (en particulier, on préfère souvent utiliser le formalisme simplifié quand on est sûr qu'il n'y a pas d'ambiguïté possible).

Quant à savoir comment ces deux points de vue sont enseignés, c'est une toute autre histoire. Personnellement j'ai lutté pendant assez longtemps avant que la chose ne devienne claire dans mon esprit, mais pour certaines personnes ça coule de source immédiatement. Mais j'insiste, il ne s'agit absolument pas de dire que les maths et la physique n'ont aucun rapport, juste de dire que les deux disciplines ont chacune leur langage (et j'ai déjà essayé de te faire comprendre ça, sans succès, dans des discussions précédentes, notamment sur l'utilisation du signe d'égalité). Les mots "livre" et "book" sont différents, mais ça ne veut pas dire que les livres outre-Manche n'ont rien à voir avec les nôtres (d'ailleurs il existe aussi en maths des notations "anglaises" et "françaises" différentes pour les mêmes objets).

[alex769]

Merci à vous tous pour ces éclaircissements, j'y vois déjà un peu plus clair.

Par contre le second exemple de Skullkid met en avant un autre "problème" sur lequel je n'ai là encore pas les idées claires. En effet l'équation dE/dt=dE/dt.dt+dE/dx.dx/dt provient pour moi de la différentielle de E que l'on a ensuite divisée par dt.
Je ne vois donc pas en quoi elle sous-entend que E est une fonction d'une seule variable.

[Dlzlogic]

Bon, je vais juste donner mon explication personnelle : puisque la dérivée, ou la différentielle (juste question de terme) est un infiniment petit, un infiniment petit du second ordre est négligeable.
Je sais que cette explication relève de l'hérétisme condamnable, donc, par avance, j'avoue. :doh:

PS. Définition de l'hérérisme (bientôt dans le dictionnaire) idée manifestement hérétique. :dodo:

[Skullkid]

Merci à vous tous pour ces éclaircissements, j'y vois déjà un peu plus clair.

Par contre le second exemple de Skullkid met en avant un autre "problème" sur lequel je n'ai là encore pas les idées claires. En effet l'équation dE/dt=dE/dt.dt+dE/dx.dx/dt provient pour moi de la différentielle de E que l'on a ensuite divisée par dt.
Je ne vois donc pas en quoi elle sous-entend que E est une fonction d'une seule variable.

La notation dy/dx utilisée en maths désigne la dérivée (ce qui n'est pas la même chose qu'une différentielle - en maths comme en physique - n'en déplaise à Dlzlogic, la dérivée d'une longueur par rapport à un temps c'est une vitesse, la différentielle d'une longueur par rapport à n'importe quoi c'est une longueur) de la fonction y d'une seule variable x. Cela dit ça reste une notation peu prisée par les matheux puisqu'elle fait apparaître le nom de la variable alors que le nom de la variable ne devrait rien avoir à faire dans l'histoire.

L'idée même de "diviser par dt" est propre au formalisme physicien. Tu peux t'en convaincre en essayant de donner une définition mathématique rigoureuse de dt et d'essayer de justifier les changements de variables multiples. Par exemple le changement en polaires x = r*cos(t) et y = r*sin(t), comment justifier que dx*dy = r*dr*dt ?

[alex769]

La notation dy/dx utilisée en maths désigne la dérivée (ce qui n'est pas la même chose qu'une différentielle - en maths comme en physique - n'en déplaise à Dlzlogic, la dérivée d'une longueur par rapport à un temps c'est une vitesse, la différentielle d'une longueur par rapport à n'importe quoi c'est une longueur) de la fonction y d'une seule variable x. Cela dit ça reste une notation peu prisée par les matheux puisqu'elle fait apparaître le nom de la variable alors que le nom de la variable ne devrait rien avoir à faire dans l'histoire.

L'idée même de "diviser par dt" est propre au formalisme physicien. Tu peux t'en convaincre en essayant de donner une définition mathématique rigoureuse de dt et d'essayer de justifier les changements de variables multiples. Par exemple le changement en polaires x = r*cos(t) et y = r*sin(t), comment justifier que dx*dy = r*dr*dt ?

Il semblerai que mes connaissances (ou mon manque de connaissance) mathématiques ne s'arrête pas à des problèmes d'interprétation des différentielles car en essayant de calculer de dx*dy je ne retrouve absolument pas le même résultat.

D'après mes calculs je trouve:
dx=cos(t).dr-sin(t)*r.dt
dy=sin(t).dr+cos(t)*r.dt
=>dx*dy=[cos²(t)-sin²(t)]*r*dr*dt+cos(t)*sin(t)*[dr*dr-r²*dt*dt]

à partir de là quelques soient les simplifications que je réalise je n'arrive pas à retrouver le même résultat que celui énoncé: dx*dy = r*dr*dt.

[Skullkid]

à partir de là quelques soient les simplifications que je réalise je n'arrive pas à retrouver le même résultat que celui énoncé: dx*dy = r*dr*dt.

Rassure-toi, c'est normal. C'est dû au fait que tous ces dx, dy, dr et compagnie, dont on s'est toujours bien gardé de te préciser la nature, sont des objets qui ne sont pas si intuitifs que ça. Bien qu'ils aient été inventés pour traduire l'idée de "nombre infiniment petit", on ne peut pas les manipuler comme on manipule les nombres habituels. Pourquoi ? "Parce que c'est comme ça" est malheureusement la seule réponse possible si on ne veut pas mettre les mains dans le cambouis mathématique qui se cache derrière.

La simplification du formalisme a un coût : on est obligé de rajouter, un peu artificiellement, des règles de calcul ad hoc pour retomber sur ses pattes. Par exemple, la justification du dx*dy = r*dr*dt pour un physicien sera de raisonner sur les petites surfaces balayées lorsqu'on fait varier chacune des coordonnées d'un pas infiniment petit : quand je choisis une abscisse dans [x,x+dx] et une ordonnée dans [y,y+dy] je balaye un petit rectangle d'aire dx*dy, quand je choisis un rayon polaire dans [r,r+dr] et un angle polaire dans [t,t+dt] je balaye un petit rectangle d'aire dr*r*dt.

[Doraki]

En particulier, si tu utilises la "règle" dtruc * dmachin = - dmachin * dtruc, (qui implique dtruc * dtruc = 0), tu devrais tomber sur le bon résultat.

[alex769]

rebonjour,

suite aux deux dernières réponses j'aurais (encore) des questions.

@Skullkid: en reprenant ton analyse "géométrique" j'obtiens en toute rigueur mathématique la formule suivante pour l'élément de surface en coordonnées cylindriques: drdt=rdrdt+dtdrdr/2. Je me rappelle bien avoir entendu dire que dtdrdr est négligeable devant rdrdt (infiniment petit d'ordre supérieur) mais je ne vois pas la rigueur mathématique ici.
Après, si mathématiquement il est prouvé que drdr = 0 comme le suggère Doraki, alors là il n'y a plus de problème.

@Doraki: la règle que tu as énoncée est-elle mathématiquement rigoureuse ou est-ce une approximation comme les infiniment petits d'ordre supérieur?

[Skullkid]

@Skullkid: en reprenant ton analyse "géométrique" j'obtiens en toute rigueur mathématique la formule suivante pour l'élément de surface en coordonnées cylindriques: drdt=rdrdt+dtdrdr/2. Je me rappelle bien avoir entendu dire que dtdrdr est négligeable devant rdrdt (infiniment petit d'ordre supérieur) mais je ne vois pas la rigueur mathématique ici.

C'est normal, il n'y a pas de rigueur mathématique dans cette justification physique. Par principe, à partir du moment où tu prétends faire des calculs sur des objets que tu n'as pas définis, tu bouscules la rigueur mathématique. Si tu veux de la rigueur mathématique, tu as deux solutions :

1 - Tu abandonnes l'idée même que les dmachin et dtruc sont des objets manipulables. En effet, on ne te les a jamais définis. Tout ce qu'on t'a défini c'est l'intégrale d'une fonction f sur un domaine D, qui peut se noter ou tout simplement . Naturellement, cette intégrale ne dépend que de f et du domaine d'intégration D, le dxdy qui apparaît dans la première notation est là uniquement pour indiquer les variables d'intégration, au cas où l'expression f(x,y) ferait apparaître d'autres lettres que x et y.

Il y a alors un théroème de changement de variable - démontrable en toute rigueur et sans jamais parler de dx et dy - qui dit que si tu as une fonction g de R^2 dans R^2 qui vérifie de bonnes propriétés (cette fonction représente ton changement de variable) alors , où ce detJ_g est une fonction (qui s'appelle le jacobien de g) qui s'exprime en fonction des dérivées partielles de g. Dans le cas où g est le passage en polaires, g(r,t) = (r*cos(t),r*sin(t)), son jacobien est detJ_g(r,t) = r.

2 - Tu ouvres un cours sur les formes différentielles où tu pourras trouver des définitions propres de dx et compagnie. Ce ne sont pas des nombres mais des fonctions à valeurs dans un espace de fonctions (ainsi dx est une fonction, dx(x,y) est encore une fonction, et (dx(x,y))(x',y') est un nombre), pour lesquelles on peut définir un produit spécial (qui n'est évidemment pas le produit sur les réels) qui vérifie notamment dx*dy + dy*dx = 0.

La première solution te sera probablement imposée si tu suis un cours de maths sur l'intégration avec le formalisme moderne. Mais il faudra de toute façon que tu t'habitues au formalisme physicien, c'est-à-dire que tu acceptes quelques écarts de rigueur, en restant cependant assuré qu'au final tes résultats sont corrects, parce qu'il y a des matheux qui ont vérifié proprement que tout ça se goupillait bien.