Bonsoir, :happy3:
Ces notations prennent leurs origines de la notion des
- formes différentielles sur un ouvert
de
.
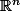
Une forme différentielle sur l'ouvert
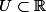
est une application :
 $)
telle que
:
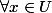
 \in \mathcal{L} ( \mathbb{R}^n , \mathbb{R} ) $)
: une forme linéaire. Dans ton cas, ton
est représenté par
, ce n'est pas un vecteur, mais un point de
.
 $)
donc appartient à l'espace vectoriel
 $)
qui est l'espace des formes linéaires, donc admet une base duale :
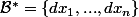
telle que :
 = dx_i (v_{1} , ... , v_n ) = v_i $)
( Ici,
est un vecteur de
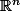
et non un point de l'ouvert
comme c'est le cas de
, ou de ton point
). Les
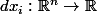
sont des formes linéaires car appartiennent à l'espace des formes linéaires
. Ce sont donc, tout simplement des projections vectorielles.
Donc
s'écrit finalement dans la base duale de la manière suivante :
 = a_1 (x) dx_1 + ... + a_n (x) dx_n $)
(
au départ était un point fixe, mais, on peut le faire varier, et on obtient
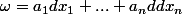
avec
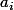
des fonctions, et non des scalaires ). On appelle
forme différentielle. Donc, pour résumer :
est une forme différentielle, mais
est une forme linéaire. mais, puisque
, si on prend un vecteur
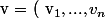 \in \mathbb{R}^n ) $)
, alors :
 (v) = \omega (x) (v_1 , ... , v_n ) \in \mathbb{R} $)
.
Par ailleurs, si
 $)
, alors sa différentielle est en un point
de
est une forme linéaire qui s'écrit :
 = \frac{\partial f}{\partial x_{1}}(a) dx_1 + ... + \frac{\partial f}{\partial x_{n}}(a) dx_n $)
, et
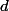
est une
- forme différentielle. On a :
(v) = df(a) (v_1 , ... , v_n ) = \frac{\partial f}{\partial x_{1}}(a) dx_1 (v_1 , ... , v_n ) + ... + \frac{\partial f}{\partial x_{n}}(a) dx_n (v_1 , ... , v_n ) = \frac{\partial f}{\partial x_{1}}(a) v_1 + ... + \frac{\partial f}{\partial x_{n}}(a) v_n $)
Si :
, alors
 = \frac{\partial f}{\partial x}(a) dx $)
, et donc :
(1) = \frac{\partial f}{\partial x}(a) dx (1) = \frac{\partial f}{\partial x}(a). 1 = = f'(a).1 $)
d'où :
 = \frac{\partial f}{\partial x}(a) = f'(a) $)
, avec d'autres notations, on note :
 = f'(a) $)
, d'où
(
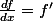
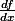
, est donc, une fonction, et non, le quotient de deux scalaires, comme c'est le cas de
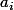
dans les
- formes différentielles. Souviens toi, tout à l'heure, on avait :
) donc, on ne peut pas écrire :
 = \frac{d f(a)}{d x (a)} $)
. Pour s'en convaincre, les formes linéaires
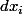
: éléments de la base duale dans
, comme je t'ai expliqué tout à l'heure, reçoivent des vecteurs
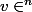
, et non, des points
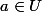
, et on écrit
 = dx(v_1 , ... , v_n ) = v_i $)
et non
 $)
qui n'a pas de sens.
J'espère que ça répond à tes attentes.
Cordialement. :happy3:
