Bonjour,
Je revise en ce moment la différentiabilité, et j'avoue que j'ai du mal a assimiler les notions du cours. J'ai cherché un peu sur internet mais des choses restent toujours très floues pour moi.
- Est-ce qu'une fonction différentiable, est juste une fonction dérivable sur un espace de dimension supérieure à 1 ?
- La dérivée directionnelle en a vers v correspond à la somme des dérivées partielles en a vers v ?
- Et plus généralement, à quoi correspond la direction de la différentielle, je comprends que c'est un vecteur, mais si la différentielle est en fait une dérivée (?), je ne comprends pas cette notion de direction
Merci pour votre aide
Différentiabilité
2 messages
- Page 1 sur 1
Re: Différentiabilité
Salut,
Visiblement, tu mélange tout . . .
Lorsque l'on a une application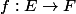 ce que l'on appelle en général "la dérivée" de
ce que l'on appelle en général "la dérivée" de  en un point
en un point 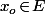 , c'est
, c'est -f(x_o)}{h}) . Sauf que, si tu regarde cette formule (et que tu la comprend . . . ), ben il faut bien voir que pour qu'elle ait du sens, ça demande des hypothèses concernant les espaces
. Sauf que, si tu regarde cette formule (et que tu la comprend . . . ), ben il faut bien voir que pour qu'elle ait du sens, ça demande des hypothèses concernant les espaces  et
et  , à savoir :
, à savoir :
- Pouvoir ajouter des éléments de pour calculer
pour calculer  .
.
- Pouvoir soustraire des éléments de pour calculer
pour calculer -f(x_o)) .
.
- Pouvoir diviser des éléments de F par des éléments de E pour diviser-f(x_o)) par
par  .
.
- Pouvoir calculer des limites donc avoir une notion de distance entre les points (de E et de F).
Et le point souligné signifie en particulier qu'on ne risque pas de calculer la "dérivée" de, par exemple, une fonction de R^2 dans R^3 (tu sait diviser un vecteur de R^3 par un vecteur de R^2 ?).
Bref, pour pouvoir faire tout les calculs et évaluer la limite, le contexte "qui va bien", c'est celui où E=R (ou C) et où F est un espace vectoriel (normé) vu qu'on sait diviser un vecteur par un réel.
1) Donc, non, une fonction différentiable, c'est surement pas "juste une fonction dérivable" vu qu'une fonction dérivable, ça doit avoir comme ensemble de départ R alors que justement, la notion de fonction différentiable a été inventé pour faire un truc qui ressemble à de la dérivation, mais avec un ensemble de départ autre que R.
2) Je comprend pas ta deuxième question vu que je vois franchement pas ce que peut être la notion de "dérivées partielles en a vers v". La notion de dérivée directionnelle, c'est simple : si tu as f:E->F où E est un e.v. différent de R, tu ne peut pas calculer de "dérivée" de f (voir çi dessus) vu que ton espace de départ est trop gros. Mais, si tu as une fonction :R->E alors la composée f
:R->E alors la composée f va de R dans F donc on peut parler de dérivée de cette fonction. Et, clairement, les fonctions les plus simples
va de R dans F donc on peut parler de dérivée de cette fonction. Et, clairement, les fonctions les plus simples  :R->E, c'est celle de la forme
:R->E, c'est celle de la forme  (avec
(avec  ) qui paramétrisent la droite passant par
) qui paramétrisent la droite passant par  dirigée par
dirigée par  . Et la "dérivée directionnelle" de f en
. Et la "dérivée directionnelle" de f en  suivant la direction
suivant la direction  , c'est la dérivée en t=0 de cette composée, c'est à dire de
, c'est la dérivée en t=0 de cette composée, c'est à dire de ) .
.
3) Je comprend pas non plus la question vu que je vois pas ce que désigne la "direction de la différentielle" : la différentielle d'une application d'une partie U de E dans F (espaces vectoriels normés), c'est une application linéaire de E dans F donc, modulo d'avoir des bases de E et de F, c'est une matrice (la matrice Jacobienne plus précisément). Et je vois pas ce que peut désigner la "direction" d'une matrice . . .
Visiblement, tu mélange tout . . .
Lorsque l'on a une application
- Pouvoir ajouter des éléments de
- Pouvoir soustraire des éléments de
- Pouvoir diviser des éléments de F par des éléments de E pour diviser
- Pouvoir calculer des limites donc avoir une notion de distance entre les points (de E et de F).
Et le point souligné signifie en particulier qu'on ne risque pas de calculer la "dérivée" de, par exemple, une fonction de R^2 dans R^3 (tu sait diviser un vecteur de R^3 par un vecteur de R^2 ?).
Bref, pour pouvoir faire tout les calculs et évaluer la limite, le contexte "qui va bien", c'est celui où E=R (ou C) et où F est un espace vectoriel (normé) vu qu'on sait diviser un vecteur par un réel.
1) Donc, non, une fonction différentiable, c'est surement pas "juste une fonction dérivable" vu qu'une fonction dérivable, ça doit avoir comme ensemble de départ R alors que justement, la notion de fonction différentiable a été inventé pour faire un truc qui ressemble à de la dérivation, mais avec un ensemble de départ autre que R.
2) Je comprend pas ta deuxième question vu que je vois franchement pas ce que peut être la notion de "dérivées partielles en a vers v". La notion de dérivée directionnelle, c'est simple : si tu as f:E->F où E est un e.v. différent de R, tu ne peut pas calculer de "dérivée" de f (voir çi dessus) vu que ton espace de départ est trop gros. Mais, si tu as une fonction
3) Je comprend pas non plus la question vu que je vois pas ce que désigne la "direction de la différentielle" : la différentielle d'une application d'une partie U de E dans F (espaces vectoriels normés), c'est une application linéaire de E dans F donc, modulo d'avoir des bases de E et de F, c'est une matrice (la matrice Jacobienne plus précisément). Et je vois pas ce que peut désigner la "direction" d'une matrice . . .
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
