Différence entre CLU et CU (convergence)

[Cryptocatron-11]

Re bonjour,

quelle est la différence entre la convergence uniforme et la convergence localement uniforme ?

Si j'en suis mon cours , on parle de convergence locale unfiforme quand la suite fn converge uniformément sur tout segment d'un intervalle I.
On parle de convergence uniforme quand la limite quand n tend vers l'infini de sup |fn(x)-g(x)| vaut 0 .

Mais quand on a convergence local uniforme on a forcément convergence uniforme . Je vois pas pourquoi on a introduit ce CLU à quoi sert il ? pourquoi ne peut on pas toujours simplement parlé de convergence uniforme ?

Si vous avez un petit exemple pour comprendre ça serait cool
MERCI.

[Joker62]

Hello.

La convergence locale uniforme n'implique pas la convergence uniforme.
(Par contre la réciproque est vraie : CU => CLU (par restriction))

Pour voir le problème :

On pose définie sur . Cette suite de fonction converge simplement vers la fonction .

Une étude de montre que la convergence n'est pas uniforme sur 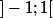(Le sup vaut plus +;))

Par contre, si on se restreint a des segments de la forme , la convergence devient uniforme.

Ainsi convergence locale sur tout segment n'implique pas forcément convergence uniforme partout.

On trouve aussi pas mal d'exemple avec l'exponentielle.

[Cryptocatron-11]

Merci Joker :lol3:

Pour trouver le sup tu as pris x = 1 c'est ça ?

[Joker62]

Pas x = 1 mais la limite quand x tend vers 1 ;)