Difféomorphisme

[Mouss75]

Bonjour à tous,

Je me pose la question suivante. J'ai une application de dans . Chacune des n fonctions de l'application est dérivable et continue (bon, on lui donne toutes les propriétés qu'il faut en fait).
Est ce que le fait que le simple fait que chaque dérivée soit de signe constant ,pas forcément le même entre les fonctions...!) est suffisant pour que mon application soit un difféomorphisme ?

Je ne trouve pas beaucoup de propriétés sur ces bestioles là, et je n'en suis pas familier..
Est ce que quelqun peut confirmer/infirmer cette assertion ?

[abcd22]

Bonjour,
Je suppose que tu parles d'une fonction , avec n > 1.
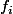
Dans ce cas les fonctions sont des applications de dans , donc elles n'ont pas de dérivée mais une différentielle (qui est une application linéaire de dans ), et ça n'a pas de sens de parler du signe d'une application linéaire.
La notion correspondante à « dérivée de signe constant » pour les fonctions de plus d'une variable est « différentielle inversible », le théorème d'inversion globale dit que :
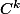
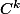
Si f est une application injective de classe de dans et que la différentielle de f en tout point x de est inversible, alors f est un -difféomorphisme (de sur son image, pas forcément de sur lui-même).
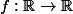
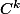
Si n = 1 on retrouve bien ce le résultat qu'on connait pour les fonctions d'une variable réelle : si est de classe , la différentielle en un point a est l'application , elle est inversible si et seulement si f'(a) est non nul.