Diagonaliser matrice

[saroon]

bonjour,

j'ai un petit problème avec la diagonalisation d'une matrice

A= 7/9 4/9 - 4/9
4/9 1/9 8/9
-4/9 8/9 1/9

voici le polynôme caractéristique que je trouve:

P(x)= 7/9-X ((1/9-X)² - 8/9²) - 4/9 ((4/9 * 1/9-X)+(4/9*8/9)) + 4/9 (4/9*8/9)+(4/9*1/9-X).

(j'ai essayé de développer par apport à la 1ère ligne)

mais est-ce vraiment la seule solution ?? je demande cela car je ne sais pas résoudre les équations de 3ème degré.

[Nightmare]

Salut,

déjà, il aurait été judicieux d'écrire et de diagonaliser B, ça évite toutes les fractions dans le calcule du polynôme caractéristique !

[saroon]

A= ( 7 4 - 4 )
1/9 * ( 4 1 8 )
( -4 8 1 )

pour un polynôme caractéristique de :
P(x)= 1/9 * ( 7-X ((1-X)² - 8²) - 4 ((4 * 1-X)+(4*8)) + 4 (4*8)+(4*1-X). )

c’est toujours aussi compliqué

[Nightmare]

Ben, il te reste à développer, rien de bien compliqué. Ensuite on cherche les racines.

[saroon]

est ce qu'il n'y aurait pas de moyen pour simplifier la matrice (obtenir des zero quelque part), afin de faciliter le calcul ??? :help:

[girdav]

On va exploiter l'idée de Nightmare, qui comme tout matheux qui se respecte, veut se simplifier la vie au maximum. On note 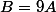, A étant la matrice de départ. À toi de trouver les valeurs propres de A en fonction de celles de B. On calcule le polynôme caractéristique de B :
.
Il ne te reste plus qu'à développer par rapport à la dernière ligne.
De manière générale, comme on veut les racines du polynôme caractéristique il vaut mieux essayer de l'avoir sous forme factorisée, i.e. essayer de trouver une ligne ou une colonne qui contient un facteur du premier degré en . Le bourrinage ne paie pas.