Diagonaliser Matrice 2*2 en devoir
13 messages
- Page 1 sur 1
Diagonaliser Matrice 2*2 en devoir
Bonjour à tous, je fais un exercice dans lequel on me demande de diagonaliser une matrice 2*2.
ça ne me parait pas compliqué, mais je me demandais si un prof pouvais donner ce type d'exo en devoir (de
2h30) (diagonaliser une matrice), sachant que ça prend du temps on dirait.
J'imagine pas pour les matrices 3*3.
Voici un exercice que j'ai entamé, j'enverrai le reste aujourd'hui ou demain normalement
j'espère que le début est bon
https://zupimages.net/viewer.php?id=23/18/mfx7.jpeg
ça ne me parait pas compliqué, mais je me demandais si un prof pouvais donner ce type d'exo en devoir (de
2h30) (diagonaliser une matrice), sachant que ça prend du temps on dirait.
J'imagine pas pour les matrices 3*3.
Voici un exercice que j'ai entamé, j'enverrai le reste aujourd'hui ou demain normalement
j'espère que le début est bon
https://zupimages.net/viewer.php?id=23/18/mfx7.jpeg
Re: Diagonaliser Matrice 2*2 en devoir
Bonjour,
Avec un peu d'entrainement, ça ne prend pas tant de temps que ça.
Pour le calcul du polynôme caractéristique, on peut ne pas s'encombrer du dénominateur 5 qui est le même pour tous les coefficients (il faut se souvenir de diviser par 5les valeurs propres). Trouver des vecteurs propres se fait à vue (là aussi ne pas s'encombrer des dénominateurs 5).
Avec un peu d'entrainement, ça ne prend pas tant de temps que ça.
Pour le calcul du polynôme caractéristique, on peut ne pas s'encombrer du dénominateur 5 qui est le même pour tous les coefficients (il faut se souvenir de diviser par 5les valeurs propres). Trouver des vecteurs propres se fait à vue (là aussi ne pas s'encombrer des dénominateurs 5).
Re: Diagonaliser Matrice 2*2 en devoir
GaBuZoMeu a écrit:Bonjour,
Avec un peu d'entrainement, ça ne prend pas tant de temps que ça.
Pour le calcul du polynôme caractéristique, on peut ne pas s'encombrer du dénominateur 5 qui est le même pour tous les coefficients (il faut se souvenir de diviser par 5les valeurs propres). Trouver des vecteurs propres se fait à vue (là aussi ne pas s'encombrer des dénominateurs 5).
Merci pour ton aide habituelle, oui je me disais bien que ce 5 me gênais, je vais m'entrainer encore.
Euh du coup bin je vais recalculer avec ta méthode , ça ira plus vite!
Re: Diagonaliser Matrice 2*2 en devoir
quelques rappels sur les matrices )
leur polynome carractéristique estX+det(A)=X^2-(a+d)X+ad-bc)
leur inverse est}\left(\begin{array}{cc}d&-b\\-c&a\end{array}\right))
après avoir divisé par det(A) on observe que:
les coeff de la diagonale principale changent de place mais pas de signe
les coeff de l'autre diagonale changent de signe mais pas de place
Ton exo devient plus simple en utilisant ces rappels
leur polynome carractéristique est
leur inverse est
après avoir divisé par det(A) on observe que:
les coeff de la diagonale principale changent de place mais pas de signe
les coeff de l'autre diagonale changent de signe mais pas de place
Ton exo devient plus simple en utilisant ces rappels
Re: Diagonaliser Matrice 2*2 en devoir
tournesol a écrit:quelques rappels sur les matrices
leur polynome carractéristique est
leur inverse est
après avoir divisé par det(A) on observe que:
les coeff de la diagonale principale changent de place mais pas de signe
les coeff de l'autre diagonale changent de signe mais pas de place
Ton exo devient plus simple en utilisant ces rappels
Bonjour tournesol, merci pour ton rappel bien utile, je connaissais seulement une des formules.
Je viens de voir ton rappel mince, bon je vais refaire avec ta méthode:
Pour l'instant voici ce que j'avais trouvé c'est pas totalement rédigé
https://zupimages.net/viewer.php?id=23/18/8nxi.jpeg
Re: Diagonaliser Matrice 2*2 en devoir
Conserve ton dénominateur
)
Polynôme caractéristique:
 ssi
ssi 
Les racines:
Un vecteur propre simple associé à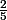 :...
:...
Un vecteur propre simple associé à 1:...
Ta matrice
Son inverse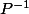
Tu vérifies queP^{-1}=A)
Tu calcules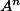
Polynôme caractéristique:
Les racines:
Un vecteur propre simple associé à
Un vecteur propre simple associé à 1:...
Ta matrice
Son inverse
Tu vérifies que
Tu calcules
Re: Diagonaliser Matrice 2*2 en devoir
Ow merci mon ami, t'as pris quelque minute pour ce qui me prend des heures
Re: Diagonaliser Matrice 2*2 en devoir
J'avais pourtant buien écrit "il faut se souvenir de diviser par 5les valeurs propres".
Pour la recherche des vecteurs propres, on peut bien rester avec , ça économise l'écriture.
, ça économise l'écriture.
Pour la recherche des vecteurs propres, on peut bien rester avec
Re: Diagonaliser Matrice 2*2 en devoir
Bonsoir GaBuZoMeu
On a en dimension qcq pour tout réel a non nul
l valeur propre de u et x vecteur propre associé ssi al valeur propre de au et x vecteur propre associé.
mais je pense que c'est peu connu.
On a aussi en dimension n :=l^n det(A))
On a en dimension qcq pour tout réel a non nul
l valeur propre de u et x vecteur propre associé ssi al valeur propre de au et x vecteur propre associé.
mais je pense que c'est peu connu.
On a aussi en dimension n :
Modifié en dernier par tournesol le 08 Mai 2023, 10:00, modifié 1 fois.
Re: Diagonaliser Matrice 2*2 en devoir
C'est pourtant une simple question de bon sens, si on sait ce que sont les éléments propres.
Re: Diagonaliser Matrice 2*2 en devoir
GaBuZoMeu a écrit:J'avais pourtant buien écrit "il faut se souvenir de diviser par 5les valeurs propres".
Pour la recherche des vecteurs propres, on peut bien rester avec, ça économise l'écriture.
J'ai pris en compte ton conseil (voir première photo) mais je ne suis pas un grand matheux, je ne suis pas habitué avec ces calcul, je vais m'entrainer encore
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
