Bonjour,
J'ai une matrice A carrée d'ordre n nilpotente de rang 1 et une matrice B carrée d'ordre n inversible. Je cherche une condition nécessaire et suffisante pour que A+B soit diagonalisable.
J'ai fait le cas particulier B=I qui fonctionne bien: A+I est diagonalisable si et seulement si A l'est ce qui donne tr(A) non nulle.
Mais je ne vois pas comment relier ce cas particulier au cas plus général souhaité. J'ai écrit A+B = B(B^(-1)A+I) et si A et B commutent alors B^(-1)A est nilpotente de rang 1 mais que faire ensuite avec le produit par B? Et sinon je n'ai pas d'idée.
Quelqu'un peut-il me donner une piste à suivre?
Merci.
Diagonalisation d'une somme de matrices
4 messages
- Page 1 sur 1
Salut,
Déjà, un premier "rappel" : une matrice nilpotente a comme seule et unique valeur propre 0 donc sa trace (qui est la somme des v.p. comptées avec ordre de multiplicité) est forcément nulle donc dans le cas où B=Id, B+A n'est jamais diagonalisable (c'est en fait le "bloc générique" dans la décomposition de Jordan).
Après, je ne suis pas sûr de bien comprendre la question : tu cherche des conditions de quelles forme exactement ?
Je pense qu'évidement une condition de la forme "à condition que A+B soit diagonalisable" ne te va pas (vu que ça fait pas vraiment avancer le schmilblick...)
Mais d'un autre coté, je suis à peu prés persuadé que tu ne trouvera pas de condition portant uniquement sur la matrice B et sans référence par exemple au noyau de A...
Déjà, un premier "rappel" : une matrice nilpotente a comme seule et unique valeur propre 0 donc sa trace (qui est la somme des v.p. comptées avec ordre de multiplicité) est forcément nulle donc dans le cas où B=Id, B+A n'est jamais diagonalisable (c'est en fait le "bloc générique" dans la décomposition de Jordan).
Après, je ne suis pas sûr de bien comprendre la question : tu cherche des conditions de quelles forme exactement ?
Je pense qu'évidement une condition de la forme "à condition que A+B soit diagonalisable" ne te va pas (vu que ça fait pas vraiment avancer le schmilblick...)
Mais d'un autre coté, je suis à peu prés persuadé que tu ne trouvera pas de condition portant uniquement sur la matrice B et sans référence par exemple au noyau de A...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Je ne sais pas pourquoi j'ai écrit A nilpotente. J'avais juste comme hypothèse que A est carrée d'ordre n de rang 1, ce qui me donne bien A+I diagonalisable si et seulement si A l'est donc si et seulement si tr(A) n'est pas nulle.
Désolée de cette grossière erreur.
On a donc) avec
avec  de rang 1 donc on peut appliquer le résultat sur la matrice
de rang 1 donc on peut appliquer le résultat sur la matrice  .
.
J'ai essayé de raisonner autrement en partant toujours de A diagonalisable avec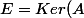\oplus Ker(A-tr(A)I)) , mais je n'arrive pas toujours à rien...
, mais je n'arrive pas toujours à rien...
Désolée de cette grossière erreur.
On a donc
J'ai essayé de raisonner autrement en partant toujours de A diagonalisable avec
Euhhh... ça aussi c'est une "très grossière erreur" : entre le fait qu'une matrice soit diagonalisable et le fait que sa trace soit (non) nulle, il n'y a aucun rapport, ni dans un sens, ni dans l'autre :kube a écrit:... si et seulement si A est diagonalisable donc si et seulement si tr(A) n'est pas nulle....
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 11 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
