Je ne connais pas de nom pour ce théorème et la seule preuve que je connaisse passe bien par les complexes.
En ce qui me concerne, je trouve la preuve assez naturelle car :
1) Il me semble assez naturel pour monter qu'un polynôme de K[X] a toutes ces racines dans K de commencer par considérer ces racines (qui sont dans la cloture algébrigue de K) PUIS de montrer qu'elles sont en fait dans K.
2) Le théorème en question peut être vu comme un cas particulier du même théorème concernant les matrices hermitiennes sur C.
Malgrés toutes ces remarques, il existe peut-être une preuve ne passant pas par la cloture algébrique...
Diagonalisation d'une matrice symétrique
10 messages
- Page 1 sur 1
bonjour
on peut le faire par récurrence sur la dim
un endo d un R ev possède un plan stable ou une droite stable
s'il y a une droite stable c est fini par récurrence l 'orthogonal étant stable par u*= u eton applique l 'hypothèse de récurrence
s'il y a un plan stable il suffit d écrire la matrice de la restriction au plan pour voir qu'il y a bien la encore des valeurs propres réelles
et on revient au cas précédent.
on peut le faire par récurrence sur la dim
un endo d un R ev possède un plan stable ou une droite stable
s'il y a une droite stable c est fini par récurrence l 'orthogonal étant stable par u*= u eton applique l 'hypothèse de récurrence
s'il y a un plan stable il suffit d écrire la matrice de la restriction au plan pour voir qu'il y a bien la encore des valeurs propres réelles
et on revient au cas précédent.
En cherchant sur internet, je n'ai pas trouvé de texte bien clair.
Pour moi, la preuve repose sur le fait que, si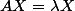 avec
avec  matrice réelle symétrique,
matrice réelle symétrique,  complexe et
complexe et  vecteur colonne complexe non nul, alors
vecteur colonne complexe non nul, alors
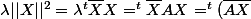X) (car A réelle symétrique)
(car A réelle symétrique) 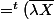X=\overline{\lambda}^t\overline{X}X=\overline{ \lambda }||X||^2) donc
donc
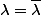 et
et  est réel (et on peut choisir
est réel (et on peut choisir  dans
dans 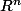 ).
).
Par contre, en cherchant, j'ai vu une autre preuve "purement réelle" : on considère le maximum de la forme quadratique associée (qui est continue) sur la sphère unité (qui est compacte)...
Pour moi, la preuve repose sur le fait que, si
Par contre, en cherchant, j'ai vu une autre preuve "purement réelle" : on considère le maximum de la forme quadratique associée (qui est continue) sur la sphère unité (qui est compacte)...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
En réfléchissant un peu, c'est assez simple :
=) donc la différentielle en
donc la différentielle en  est
est \,:\;H\mapsto +=2) car
car  symétrique.
symétrique.
Si est un max. ou min. local sur la sphère alors la différentielle doit être nulle sur l'espace tangent en
est un max. ou min. local sur la sphère alors la différentielle doit être nulle sur l'espace tangent en  à la sphère, c'est à dire que l'on doit avoir
à la sphère, c'est à dire que l'on doit avoir 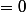 pour tout
pour tout  tel que
tel que 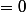 . Cela implique bien que
. Cela implique bien que =\lambda X) avec
avec  dans
dans  .
.
Si
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
