Diagonalisation
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par legeniedesalpages » 08 Jan 2008, 11:49
par legeniedesalpages » 08 Jan 2008, 11:49
Bonjour, je coince sur cet exercice:
On travaille ici avec
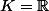
. On suppose que
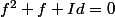
.
a. Est-ce que f est diagonalisable?
b. Déterminer
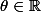
pour lequel on a:
} (\sin(n\theta)f - \sin((n-1)\theta)Id)
) pour tout
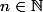
. Est-ce que cette égalité s'étend à

.
Je ne saisis pas vraiment pour la a. Avant on calculait le polynôme caractéristique pour voir si un endomorphisme est diagonalisable. Là apparemment il faut faire autre chose mais je vois pas vraiment quoi.
Merci pour votre aide.
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 08 Jan 2008, 12:15
par alben » 08 Jan 2008, 12:15
Bonjour
en multipliant les deux membres de f²+f+I=0 par (f-I), on arrive à f^3=I, ça semble curieux si les corps des scalaires est R
Tu peux supposer que f est diagonalisable, donc s'écrit... et la relation ci-dessus te conduit à une contradiction
-
klevia
- Membre Relatif
- Messages: 318
- Enregistré le: 04 Oct 2007, 20:00
-
 par klevia » 08 Jan 2008, 13:00
par klevia » 08 Jan 2008, 13:00
Salut, on a le théorème suivant :
f diagonalisable <=> son polynome minimal est scindé à racines simples.
Ici, X²+X+1 est un polynome annulateur de f non factorisable dans R donc c'est le polynome minimal de f donc f n'est pas diagolisable .
 par legeniedesalpages » 08 Jan 2008, 22:46
par legeniedesalpages » 08 Jan 2008, 22:46
pour la b., je suis perdu, quel rapport il y a entre l'endomorphisme f et des sinus? :hein:
 par legeniedesalpages » 08 Jan 2008, 23:08
par legeniedesalpages » 08 Jan 2008, 23:08
b. Déterminer
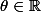
pour lequel on a:
} (\sin(n\theta)f - \sin((n-1)\theta)Id)
) pour tout
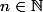
. Est-ce que cette égalité s'étend à

.
Bon déjà pour voir si f est bijective, et là je vois pas ce qui permet de nous le dire.
Enuite peut être faut-il que je me serve du fait que
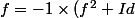)
, et donc
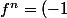^n\times(f^2+Id)^n)
.
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 08 Jan 2008, 23:16
par kazeriahm » 08 Jan 2008, 23:16
salut
on a -f^2-f=Id donc f(-f-Id)=Id donc f est inversible
-
achille
- Membre Naturel
- Messages: 94
- Enregistré le: 27 Juin 2007, 11:21
-
 par achille » 08 Jan 2008, 23:23
par achille » 08 Jan 2008, 23:23
klevia a écrit:Salut, on a le théorème suivant :
f diagonalisable son polynome minimal est scindé à racines simples.
attention pas d'équivalence, la matrice nulle est very diagonalisable sans pour autant avoir un polynome carac à racines simple : il est (-X)^n, mais le sens <= est juste, et il fait l'affaire pour la première question considérant le corps....
 par legeniedesalpages » 08 Jan 2008, 23:29
par legeniedesalpages » 08 Jan 2008, 23:29
achille a écrit:attention pas d'équivalence, la matrice nulle est very diagonalisable sans pour autant avoir un polynome carac à racines simple : il est (-X)^n, mais le sens <= est juste, et il fait l'affaire pour la première question considérant le corps....
non mais pour le polynôme minimal il y a bien équivalence.
 par legeniedesalpages » 08 Jan 2008, 23:31
par legeniedesalpages » 08 Jan 2008, 23:31
kazeriahm a écrit:salut
on a -f^2-f=Id donc f(-f-Id)=Id donc f est inversible
ah d'accord, merci.
Tu aurais une piste à me donner pour la formule avec le sinus? je dois faire une genre de binôme de Newton?
-
achille
- Membre Naturel
- Messages: 94
- Enregistré le: 27 Juin 2007, 11:21
-
 par achille » 08 Jan 2008, 23:47
par achille » 08 Jan 2008, 23:47
legeniedesalpages a écrit:non mais pour le polynôme minimal il y a bien équivalence.
sory j'ai cru avoir lu polynom carac...
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 09 Jan 2008, 00:39
par kazeriahm » 09 Jan 2008, 00:39
deja pour n=2 tu as
f^2=1/sin(theta)*(sin(2theta)f-sin(theta)*Id))
Donc 2*cos(theta)=-1 (si theta existe), et theta=+-Pi/3 [2Pi]
De plus il est clair que si theta convient, -theta aussi. Donc si theta existe theta=+-Pi/3 [2Pi].
Maintenant je pense qu'une récurrence permet de conclure.
 par legeniedesalpages » 09 Jan 2008, 11:13
par legeniedesalpages » 09 Jan 2008, 11:13
kazeriahm a écrit:deja pour n=2 tu as
f^2=1/sin(theta)*(sin(2theta)f-sin(theta)*Id))
Donc 2*cos(theta)=-1 (si theta existe), et theta=+-Pi/3 [2Pi]
De plus il est clair que si theta convient, -theta aussi. Donc si theta existe theta=+-Pi/3 [2Pi].
Maintenant je pense qu'une récurrence permet de conclure.
ok merci je regarde ça, par contre ce serait plutôt
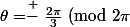)
, non?
 par legeniedesalpages » 09 Jan 2008, 11:55
par legeniedesalpages » 09 Jan 2008, 11:55
par contre j'ai du mal à montrer l'hérédité pour la récurrence,
ie si c'est vérifié jusqu à l'entier n, comment montrer que c'est vérifié pour n+1 ?
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 09 Jan 2008, 12:35
par kazeriahm » 09 Jan 2008, 12:35
j'aurais dit avec le binome de Newton, sans garanti
 par legeniedesalpages » 09 Jan 2008, 15:28
par legeniedesalpages » 09 Jan 2008, 15:28
ok merci kazeriahm, je regarderai ça plus tard.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
