Diagonalisation de matrice

par **audre66** » 08 Juin 2007, 19:02

bonjour
dans un exo j'ai

1 0 0
A= 0 -2 -1
0 1 2
on me demande si elle est diagonisable
pour ça je doit trouver les valeur propre puis les vecteurs prope et ensuite je fai quoi?
merci

par **nekros** » 08 Juin 2007, 19:06

Salut

Le polynôme caractéristique vaut :

Il est scindé à racine simple, donc A est diagonalisable.

par **audre66** » 08 Juin 2007, 19:21

recoucou et pourquoi racine de 3 ?

par **nekros** » 08 Juin 2007, 19:23

Bah ça vient du polynôme caractéristique.

En fait on a

Tu arrives à le calculer ou pas ?

par **audre66** » 08 Juin 2007, 19:29

non j'arrive pas je croyais que le polynome était
(1-alpha)(-2-alpha)(2-alpha)

par **aviateurpilot** » 08 Juin 2007, 19:37

audre66 a écrit:non j'arrive pas je croyais que le polynome était
(1-alpha)(-2-alpha)(2-alpha)

par **nekros** » 08 Juin 2007, 19:43

audre66 a écrit:non j'arrive pas je croyais que le polynome était
(1-alpha)(-2-alpha)(2-alpha)

Ca n'est pas possible !

Le terme constant est

Or,

et toi tu as

par **audre66** » 08 Juin 2007, 19:53

si on reprend du début comment je doit faire ? merci

par **aviateurpilot** » 08 Juin 2007, 20:00

audre66 a écrit:si on reprend du début comment je doit faire ? merci

calcule ce determinant

par **nekros** » 08 Juin 2007, 20:03

Oui en plus là c'est facile il suffit de développer par rapport à la première ligne.

par **audre66** » 08 Juin 2007, 20:04

le probleme c que je ne sais pas comment on calcule le det je suis désolé de vous embété mais je pete un boulon merci de vos réponse

par **audre66** » 08 Juin 2007, 20:17

comment calcule t on le det?
merci

par **kazeriahm** » 08 Juin 2007, 20:40

c difficile a expliquer au travers d'un pc, il y a plusieurs manieres.

cherche sur http://www.wikipedia.org

par **muse** » 09 Juin 2007, 10:42

Le calcule du determinant est tres important si tu ne sais pas le faire tu ne pourra pas faire beaucoup de chose

Donc une fois que tu saura le faire :

Calculer le determinant de A-xid: tu ecrit A et tu fais -x sur la diagonale

Une fois que tu as le determinant tu t'apercois que c'est un polynome de degres egal ou inferieur a la taille de la matrice en general...

Donc tu as une matrice 3-3 donc tu aura surement un polynome de degres trois.

Tu cherches les solutions a ton polynome =0 et tes solutions sont les valeurs propres.

Ensuite tu calcules le noyau de A-x id avec x les valeurs propre. Et ta aura surement un vecteur qui sera un vecteur propre...

Tu fai la meme chose avec les deux autres valeurs.

Ensuite tu ecrit tes trois vecteur en collonne les uns a coté des autre et sa te donne un matrice P dite de passage.

Tu calcule l'inverse de cette matrice Q

Et par magie :

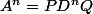
avec D la matrice diagonnale ( que des 0 sauf sur la diagonnal ou tu met les valeurs propres)

Dsl pour les fautes j'avais pas trop le temps

par **audre66** » 09 Juin 2007, 17:22

merci ta réponse est trés clair g bien compris maintenant

par **kazeriahm** » 09 Juin 2007, 17:46

muse dans ta réponse les "surement" peuvent etre remplacés par "c'est sur" :id:

par **audre66** » 13 Juin 2007, 10:41

je pense qu'il y a une erreur c pas racine de trois mais de 2 quelqu'un pourrai t il me di si g tord ou pas merci?

par **nuage** » 13 Juin 2007, 11:17

Salut,
je trouve le même résultat que nekros.

par **audre66** » 13 Juin 2007, 11:55

moi non et je comprend pas pour koi
on a (-1)^(1+1) *(1-x) det -2-x -1
1 2-x
=(1-x) [(-2-x)(2-x)-(1*-1)]
=(1-x) [(-2-x)(2-x)+1)]
jusque la tu as pareil que moi?

par **audre66** » 13 Juin 2007, 11:56

c bon je l'ai refait je trouve comme toi merci

Diagonalisation de matrice

diagonalisation de matrice

Qui est en ligne