Diagonale de Contor et non dénombrabilité de R

[banoga9892]

Bonjours, j'ai besoin d'aidre pour une preuve (je pense un classique) que je n'arrive pas à bien saisir.
Voici les étapes importantes (de ce que j'ai compris) que R est non dénombrable.

D'abord on montre qu'il y a bijection entre R et l'intervale ]0, 1[ cela se fait avec une fonction, jusqu'à la sa va. Ensuite on suppose que l'on peut dénombrer les éléments de cet intervalle pour ensuite montrer enfin que cela conduit à une contradiction avec la diagonale de Contor . Notamment, si on écrit un réel de l'intervale comme 0 . a1 a2 a3 a4 . . . alors si on listait les éléments de notre liste dénombrable de réels :
0 . a11 a12 a13 a14 . . .
0 . a21 a22 a23 a24 . . .
0 . a31 a32 a33 a34 . . .
0 . a41 a42 a43 a44 . . .
.
.
.
on peux construire un élément qui n'est pas dans cette liste en prenant 0 . b1 b2 b3 b4 . . . avec b1 différent de a11, b2 différent de a22, etc.

Or, c'est la que je comprend pas trop , je veux dire sa m'a l'aire de marcher mais sa fait vraiment des trucs bizarres. Par exemple si on créait la liste:
(0 . 1 0 0 0 0 0 0 . . .),( 0 . 2 0 0 0 0 0 0 . . .) , . . . , ( 0 . 9 0 0 0 0 0 0 . . .) ,( 0 . 1 1 0 0 0 0 0 . . .),( 0 . 1 2 0 0 0 0 0 . . .) . . .
on bref comme si je comptait de l'autre coté du point (a quelques exceptions faites) en mettant une infinité de zero a droite. En constuisant 0 . b1 b2 b3 b4 . . . , le premier élément sera effectivement différent de a11 élément, mais a22, a33 ,a44 . . . sont tous égaux a 0 , on assigne une valeur différente de zero a chaque élément, mais chaque étape de construction de ce nombre est dans la liste. Je peux aussi créer plein de listes qui ont un comportement similaire.

De la certaines hypotheses et ma premiere question: Faut il dire qu'en fait il y a beaucoups de nombres qui sont a +8 , dont le nombre que j'essaye de construire et cela se traduirait par le fait qu'il n'est pas et qu'ils ne sont pas de ce fait dans la liste . L'erreur est elle dans le fait que le nombre qui est égal au nombre que j'essaye de construire est tres loin de celui-ci (impeu exponentiellement infini plus loins) ou est ce que il y a d'autres raisons?

Apres je sais qu'il y a certaines constructions a éviter lors de la contruction de la lite , notamment celles du genre ( 0. (nombre fini de chiffres ) 9 9 9 9 . . . ) avec les 9 qui se répétent a l'infini. De la ma deuxieme question , est ce qu'il y en a d'autres qu'il faudrait éviter ? 'Merci de m'éclairer

[Kolis]

Cela serait plus lisible avec des indices à leur place, ce qui n'est pas bien difficile.

Du moment que tu choisis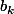 différent quel serait le numéro de ton nouveau nombre ?
Si tu dis qu'il est égal à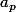 c'est faux puisque les décimales de rang sont distinctes.

[GaBuZoMeu]

banoga9892, as-tu remarqué que dans la liste que tu donnes en exemple, tous les nombres sont décimaux : ils n'ont qu'un nombre fini de décimales non nulles. Par contre, le nombre construit à partir de cette liste par le procédé diagonal de Cantor n'est pas décimal : il a une infinité de décimales non nulles.

Tu t'enfumes toi-même avec un discours trop vague.

[tournesol]

Soit une suite de réels de l'intervalle ]0;1[(ie une application de 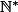dans ]0;1[
Je reprend ta notation , par exemple
On convient que les décimaux n'ont qu'un nombre fini de décimales non nulles:
par exemple 0,438 ne sera pas noté 0,4379999...
Soit le réel défini par : pour tout k 1 ,
Pour tout n 1 , on a car (r et n'ont pas la même nième décimale)
Donc il n'existe aucune application surjective de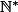 dans ]0;1[
Donc ]0;1[ n'est pas dénombrable .