Devoir Maison Somme de Polynôme.

[Aurelie]

Bonjour à tous, j'ai un Dm à faire pour la semaine prochaine en maths et je cale à un des exercices.

J'aimerais donc que vous me donniez un petit coup de main.

L'exercice est le suivant :

Soit P(X) =1+X+X^2 +X^3 +X^4

1) Montrer que P(e^(ipi/5))=2 /(1 - e^(ipi/5))

2) Calculer  Σ k=0 à 4 de cos(k*pi/5) et  Σ k=0 à 4 de sin(k*pi/5)


J'ai réussi sans trop de difficultés à faire la question 1) en remarquant que P est la somme des 5 premiers termes de la suite géométrique de raison X ainsi j'ai P(X) = (1-X^5)/(1-X) et avec X=e^(ipi/5) on a P(e^(ipi/5))=(1-e^(ipi))/(1-e^(ipi/5))=(1-(-1))/(1-e^(ipi/5))=2 /(1-e^(ipi/5))

Mais pour la question 2) je suis complètement bloqué et ne sais pas quoi faire. Je me doute qu'il faut sûrement que j'utilise ce que j'ai démontré à la question 1) mais je ne vois pas comment faire.
De plus je sais que cos(k*thêta) =Re(e^(k*i*thêta)), pareil sin(k*thêta) =Im(e^(k*i*thêta)) et la somme des deux est équivalente à  Σ k=0 à 4 de P(e^(i*k*pi/5)). Mais comment faire pour n'obtenir que cos ou que sin et surtout pour calculer ces sommes avec le résultat de la première question ???

J'espère que vous allez pouvoir m'aider de sorte que cet exercice soit plus clair pour moi et que je puisse le résoudre !!


Je vous remercie d'avance pour votre aide et votre temps accordé !!

[Ben314]

Salut,
C'est tout bon, sauf là (en rouge) :

De plus je sais que cos(k*thêta) =Re(e^(k*i*thêta)), pareil sin(k*thêta) =Im(e^(k*i*thêta)) et la somme des deux est équivalente à  Σ k=0 à 4 de P(e^(i*k*pi/5))

Si tu note tes trucs en bleu, ça dit que, pour tout , on a et, si tu somme de 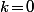à 4, ça donne et ça signifie que , c'est la partie réelle de et que , c'est la partie imaginaire de .
Et comme au 1) tu as déjà calculé , il te reste "juste" à en déterminer la partie réelle et imaginaire ce qui est très court si on utilise une petite astuce, et un peu fastidieux sans astuce (tout dépend aussi de la "forme" sous laquelle on veut écrire le résultat)

[Aurelie]

Merci beaucoup pour ton aide.

J'ai bien compris d'où venait mon erreur et ai compris ton raisonnement.

Du coup je me retrouve finalement avec 2/(1-e^(ipi/5)). Mais comment isoler la partie réelle et imaginaire ? J'ai essayer en développant mais je tourne en rond....

Pourrais tu donc me donner ta petite astuce stp ! Comment faire ce calcul avec la forme exponentielle ?

[Ben314]

La "méthode classique" pour trouver la partie réelle et imaginaire d'un complexe écrit sous la forme (avec et complexes), c'est d'écrire de façon a avoir un dénominateur réel.

Sinon, lorsque c'est possible, c'est évidement plus simple de passer par les formes polaires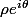 pour effectuer des multiplications/divisions. Et là, la "petite astuce", c'est que c'est la somme de deux complexes de même module donc géométriquement parlant, ça donne un losange et ça permet de voir directement quel va être un argument de la somme des deux complexes.

[Aurelie]

Merci beaucoup pour ta petite astuce.

Je vais essayer avec ça