Devoir maison de maths

[tifiore777]

Bonjour j'ai un sujet à traiter en maths j'ai essayer d'y réfléchir mais rien ne me vient Est ce que quelqu'un pourrait m'aider à réaliser ceci s'il vous plaît?

On note g la fonction définie par g=x²-lnx et la fonction f est définie par f(x)= x +(1/x) +((lnx)/x)
On note C la courbe représentative de f et D la droite d'équation y=x
1.a Déterminer le domaine de définition de g
.b Déterminer le tableau de variation complet de g (avec le limites aux bornes). En déduire le signe de g (x) suivant les valeurs de x.

2.a Déterminer le domaine de définition de f ainsi que ses variations.
b Déterminer lim lorsque x tend vers 0 de f(x) puis lorsque x tend vers + l'infini

3a. determiner lim lorsque x tend vers + l'infini de [f(x)-x] Etudier la position de C par rapport à D
b.Montrer qu'il y existe un unique point A(x0,f(x0)) de la courbe C tel que la tengente T à la courbe C en ce point soit parallèle à D .
On donnera les coordonnées de ce point , ainsi que l'équation de la courbe T de la courbe C en ce point

c.MOntrer que la courbe C coupe l'axe des abscisses en un unique point
Montrer que l’abscisse de ce point est infèrieur à (1/e)

d.Tracer dans un même repère orthonormé la courbe C, les droites D et T , ainsi que la droite d'équation x= (1/e). on donne (1/e) envrions egale à 0,37 à 0,01 près

[Mikihisa]

Tu suppose le limite de lnx/x connu ou tu dois le montrer ?

C'est la seule difficulté de l'exercice.

Ps: cet exercice est de toute évidence un exercice de lycée, pourquoi ne pas le proposer dans la section. Correspondante ?

[tifiore777]

Bonjour , Merci à vous de m'avoir répondu en effet j'aurais pu le mettre dans a rubrique lycée je m'en excuse . La lim de lnx/x est supposée connue j'ai utilisée le théorème des croissances comparées.
En faite c'est un devoir à rendre pour la rentrée en CPGE du coup j'aimerai être assez sure de ce que j'ai fait pouvez vous m'apporter votre aide s'il vous plaît?

Voilà ce que j'ai fait jusqu'à présent :

1.a La fonction g est définie pour tout x tel que lnx >= 0 équivaut à lnx>= 1 donc x>=1
Le domaine de définition de la fonction g est donc ]0;+l'infini [
deja à ce niveau j'ai l'impression qu'il manque des justifications où peut être un soucis de rédaction ?

1b.La fonction g est une fonction continue et dérivable sur son ensemble de définition :
g'(x)=2x - (1/x)

Pour étudier le signe de la dérivée plus simplement on transforme l'écriture de la fonction en la mettant au même dénominateur
g'(x)= (2x²-1)/x

Sur ]o;+ l'infini [ le dénominateur est strictement positif donc le signe de la dérivée dépend de celui du numérateur

On calcul delta delta = 9

x1= 3/4 et x2 = -3/4

J'ai obtenu un tableau de signe et de variation

lim lorsque x tend vers 0 x² -lnx = 0
On transforme l'expression x² - ln x = x (x -(lnx/x))= x (x + x ln x)
lim x=0
lim x lnx (en 0) = 0
Par somme lim x + ln x =0
Par produit lim x (x + x ln x) = 0 d'où le résultat

lim en + l'infini
lim x² -lnx = + l'infini

On transforme l'expression x² - ln x = x (x -(lnx/x))
lim x= + l'infini
lim (ln x / x) (en + l'inf )= 0
Par soustraction lim x -(lnx/x) = + l'infini
Par produit x (x -(lnx/x)) = +l'inifini

[Joker62]

Hello,

Ton raisonnement pour l'ensemble de définition est un peu suspect.
(Même faux en fait de x >= 1 tu passes à x € ]0;+\infty[ )

La continuité n'a rien à voir dans la dérivation de g.

La limite en 0+ de g n'est pas une forme indéterminée. Il ne faut donc pas transformer l'expression.

As-tu tracé la fonction sur calculatrice/géogébra pour confirmer tes dires ?

PS : Quand on doit résoudre 2x^2 - 1 = 0 (d'ailleurs tes racines sont fausses), c'est assez mal vu de faire Delta étant donné que ce genre d'équation, on sait les résoudre en seconde.

Bon courage ;)

[tifiore777]

Hello,

Ton raisonnement pour l'ensemble de définition est un peu suspect.
(Même faux en fait de x >= 1 tu passes à x € ]0;+\infty[ )

La continuité n'a rien à voir dans la dérivation de g.

La limite en 0+ de g n'est pas une forme indéterminée. Il ne faut donc pas transformer l'expression.

As-tu tracé la fonction sur calculatrice/géogébra pour confirmer tes dires ?

PS : Quand on doit résoudre 2x^2 - 1 = 0 (d'ailleurs tes racines sont fausses), c'est assez mal vu de faire Delta étant donné que ce genre d'équation, on sait les résoudre en seconde.

Bon courage

Merci beaucoup de m'avoir répondu !

Enfaite je ne sais absolument pas comment démontrer que le domaine de définition de g est ]0; + l'infi[ pouvez vous m'éclairer s'il vous plaît ?

Mince oui
lim lorsque (x tend vers 0+) x² -lnx = +l'infini

lim x²= 0
lim lnx (en 0+) = -l'infini
Par somme lim x – ln x= +l'infini d'où le résultat

AH oui erreur bête

2x²-1=0
2x²=1
x²= ½
x= -racine ½ ou racine 1/2


en tout cas merci !!!

[tifiore777]

Mince oui
lim lorsque (x tend vers 0+) x² -lnx = +l'infini

lim x²= 0
lim lnx (en 0+) = -l'infini
Par soustraction lim x² – ln x= +l'infini d'où le résultat

[Joker62]

Pour le domaine de définition, il n'y a rien à dire.
On ne peut prendre un logarithme népérien que d'un réel strictement positif.

Donc Dg = ]0;+;)[

[tifiore777]

Pour le domaine de définition, il n'y a rien à dire.
On ne peut prendre un logarithme népérien que d'un réel strictement positif.

Donc Dg = ]0;+;)[

Bonjour, et encore merci de m'avoir répondu pouvez vous encore m'aider s'il vous plaît ?
2.a Déterminer le domaine de définition de f ainsi que ses variations.
Le domaine de définion de la fonction f(x) = x+ (1/x) + (lnx/x) est ]0*; +l'infini[

f(x)= f(x) = x+ (1/x) + (lnx/x)
f('x) = 1-(1/x²) + ((x/2)-lnx)/ x²)
=(x²-1 + (x/2)-lnx/ x²)

Il faut ensuite étudier le signe de la dérivée
f'(x) est du signe du numerateur car le dénnominateur est strictement positif
x²-1 + (x/2)-lnx >0
x²-1 + (x/2)> ln x
e^(x²-1 + (x/2)) > x

j’obtiens ça mais je ne crois pas que ce soit ce qu'il faut que je fasse

Je pense que la fonction est strictement positif sur ]0;+l'infini [
mais je ne sais le justifier :/

[Joker62]

La dérivée de c'est ???

En prépa, il faut apprendre à avoir un esprit critique, apprendre à vérifier, apprendre à utiliser les outils disponibles.

Par exemple, grâce à xcas en ligne (ici) :



La dérivée de est

[deltab]

Bonsoir

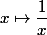
En prépa, il faut apprendre à avoir un esprit critique, apprendre à vérifier, apprendre à utiliser les outils disponibles.

en particulier l'outil informatique. mais il ne faudra pas en abuser. Cet outil n'est disponible généralement dans lex examens de mathématiques.

[tifiore777]

Ah ok merci beaucoup =)

[tifiore777]

Bonsoir , j'ai encore une dernière ou avant dernière chose à vous demander si possible s'il vous pla
enfaite je suis à la question
3.c
j'ai pu dresser au préalable le tableau de variation de la fonction f j'ai est reconnu que f'(x)= g(x)/x²
donc les variations de f sont les mqueême que celle de g c'est à dire : décroissante sur 0;racine de 2 sur 2 et croissante sur racine de 2 sur 2;plus l'infini.

mais je trouve qu'il y a un soucis car ça ne correspond pas à ce que j obtiens sur le graphique de la calculatrice la fonction est strictement croissante
pour la question 3. c MOntrer que la courbe C coupe l'axe des abscisses en un unique point
Montrer que l'abscisse de ce point est infèrieur à (1/e)

je compte utiliser le théorème des valeurs intermédiaires j'ai l'impression d'avoir fait une erreur dans mon tableau de variation franchement je suis un peu perdu pouvez vous m'aider s'il vous plaît ("encore une fois désolé )

[Joker62]

C'est parce que f' est du même signe que g.

Donc pour avoir les variations de f, il faut le signe de g.

[tifiore777]

C'est parce que f' est du même signe que g.

Donc pour avoir les variations de f, il faut le signe de g.

G est strictement positif du coup f est strictement croissante cest bien ça ?

[Joker62]

J'sais pas, selon toi ?

[tifiore777]

J'sais pas, selon toi ?

Oui oui je pense bien ^^

[Joker62]

Bon bé ok alors :)