Voilà,
Dans un magazine dédié aux sciences, j'ai trouvé cette petite énigme que je vous fais partager en espérant que quelqu'un pourra quelque peu m'éclairer :
=> Pierre partage des billes de la façon suivante : à son ami préféré, il donne 1 bille + 1/p du reste (p>2), au deuxième, il donne 2 billes + 1/p du nouveau reste; et ainsi de suite.
Après avoir servi le dernier, il lui reste 27 billes.
Combien de billes avait-il et quelle est la part de chacun ?
Merci pour votre aide
Devinette mathématique
4 messages
- Page 1 sur 1
Salut,
Si to problème est uniquement de calculer la somme, c'est assez simple.
Si on note le nombre de billes qu'il lui reste aprés avoir servi son n-ième copain, l'énoncé te dit que :
le nombre de billes qu'il lui reste aprés avoir servi son n-ième copain, l'énoncé te dit que :
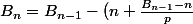<br />=(B_{n-1}-n)\lambda) où
où 
d'où (récurrence)
\lambda^2 -n\lambda=B_0\lambda^n-\lambda^{n+1}\Big(1(\frac{1}{\lambda})^1+2(\frac{1}{\lambda})^2+...+(n-1)(\frac{1}{\lambda})^{n-1}+n(\frac{1}{\lambda})^n\Big))
et tu caclule cette dernière somme en utilisant
=\frac{\partial}{\partial q}\big(\frac{1-q^m}{1-q}\big)=...)
Si to problème est uniquement de calculer la somme, c'est assez simple.
Si on note
d'où (récurrence)
et tu caclule cette dernière somme en utilisant
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
