Développements limités d'ordre 3

[adrien69]

En raquant. Et c'est cher.
Ou bien si ton lycée a un abonnement pour tous les étudiants. Demande toujours ça vaut le coup.

Franchement la méthode BlackJack est vraiment risquée. Mais c'est un point de vue.
Pour ce qui est du second résultat, il est faux. D'une part parce que tu as oublié que tu devais diviser par 3!=6 et pas 3, et d'autre part chez moi f'''(0)=456.
Je calcule f'''(x) et je te mets ça ici en éditant.

En "simplifiant" j'arrive à ça :

-(12(47sin(x)+9sin(3x)-47cos(x)+9cos(3 x)))/(sin(x)+cos(x))^9

Erreurs de calcul non impossibles.

[Luc]

Bonjour,

effectivement il y a deux méthodes pour calculer les DL en 0 :

1 - utiliser les DL connus et les multiplier pour obtenir celui cherché.
2 - calculer les dérivées n-ièmes en 0 de la fonction et remplacer dans Taylor-Young.

En pratique, dans 95% des cas, la méthode 1 est plus courte :moins de calculs à faire et donc moins de risque de se tromper. Encore faut-il connaître (par cœur) les développements limités usuels en 0.

Par exemple, voici mon calcul pour f(x)=3/(x+2)².

On factorise toujours par la partie principale (l'équivalent de f(x) en 0, ici 3/4).
.
On se retrouve donc à utiliser un DL en 0 à l'ordre 3 de , que l'on connait par cœur où qu'on lit dans les tables de DL, avec et .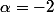

On obtient après calcul

Pour le deuxième, c'est encore du , je te laisse trouver les valeurs de u (et trouver un équivalent de u) et et donner le résultat.

Pour le troisième, c'est encore du avec , mais il faut faire attention à bien comprendre pourquoi on peut injecter un DL de u(x)=ln(1+3x) dans le DL de .

Le quatrième est une multiplication de DL usuels. Il faut bien voir à quel ordre tu as besoin de développer chaque facteur pour obtenir des termes jusqu'en o(x^3). Ça ne sert à rien de calculer les termes en x^4 par exemple. Et sur cet exemple, la méthode 1 est bien plus facile que de calculer des dérivées.

Le cinquième, c'est une composée de DL usuels, en posant u=-sin(x)