Développements asymptotiques

[MacManus]

Bonjour !

Je cherche à montrer que lorsque n

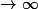
1/



2/
On pose


Pour 1/ je connais un développement limité de ln(n+1), mais je ne retrouve pas l'expression demandée.

Merci pour votre aide!

[Antho07]

Le developpement limité de ln(1+n)=n-n²/2 + .... n'est pas valable que pour n tendant vers 0.

Ici on a :



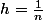
donc en posant on a quand n tend vers l'infini, h tend vers 0 et on peut utiliser le developpement limite au premier ordre de Ln(1+h) pour conclure.

[MacManus]

Merci Antho07 !

Effectivement j'avais écrit le DL de ln(1+n) à l'odre 1 lorsque n tend vers 0. Poser h = 1/n est le petit brin de folie qui me manquait. Merci ça marche en effet.

Est-ce que je peut utiliser ce résultat précédent pour montrer la 2ème égalité ? J'ai essayé mais ca ne me donne point le résultat escompté. J'aurai besoin d'un petit coup de pouce. Merci encore.