Vu que tu as l'air dêtre complètement paumé sur la façon de s'y prendre avec des factorielles, je te le fait pour le cas des impairs (plus compliqué que les pairs) :
On sait donc que, pour tout entier
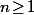
, on a
)
et on en déduit que :
^2}{3\!\times\!5}a_1\ ;\ a_7\!=\!\dfrac{\!-6}{\ 7}a_5\!=\!\dfrac{\!(-6)^3}{3\!\times\!5\!\times\!7}a_1\ ;\cdots\ ;\ <br />\red a_{2p+1}\!=\!\dfrac{\!(-6)^p}{3\!\times\!5\!\times\!7\!\times...\times\!(2p\!+\!1)}a_1)
Formule que l'on peut (que l'on doit ?) démontrer proprement par récurrence, mais le mini du mini, c'est bien évidement que cette formule "colle" avec les cas particulier donné au début !!!!
Ensuite,
)
, c'est sûrement pas la factorielle de quoi que ce soit, vu que c'est pas un produit d'entiers
successifs.
Sauf que
LA astuce à avoir vu au moins une fois, c'est que :
\big)\!\times\!\big(2\!\times\!4\!\times\!6\!\times...\times\!(2p)\big)=2\!\times\!3\!\times\!4\!\times\!5\!\times\!6\!\times...\times\!(2p)\!\times\!(2p\!+\!1)=(2p\!+\!1)!)
et que
=(2\!\times\!1)\!\times\!(2\!\times\!2)\!\times\!(2\!\times\!3)\!\times...\times\!(2\!\times\!p)=2^p\big(1\!\times\!2\!\times\!3\!\times...\times\!p)=2^p\!\times\!p!)
=\dfrac{(2p\!+\!1)!}{2^p\!\times\!p!}\ \text{ et donc que }\ a_{2p+1}\!=\!\dfrac{\!(-6)^p\!\times\!2^p\!\times\!p!}{(2p\!+\!1)!}a_1)
^p\!\times\!p!}{(2p\!+\!1)!}a_1\)
qui ne correspond à aucune série entière "classique" (mais qui, bien heureusement, "colle" avec les cas particuliers de
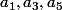
déjà évalués au dessus)
Et je t'inciterais plus que fortement à démontrer directement ce dernier résultat par récurrence en partant de la formule
) Remarque :
Remarque : Le résultat sous la forme bleue est plus "concis" à écrire que celui sous la forme rouge (et permet par exemple d'utiliser la formule de Stirling pour avoir une approximation de
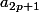
), mais il faut bien comprendre qu'il est plutôt "plus compliqué" en terme d'opérations que celui en bleue (par exemple pour un calcul explicite de
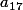
à la main ou à la machine).
