Soient
Notons
La correction indique que en supposant la somme de la série nulle, on a:
Je comprends les dernières égalités mais pas la première, où est passé le
Développement en série entière
2 messages
- Page 1 sur 1
Développement en série entière
par ArtyB » 16 Mai 2018, 11:08
Bonjour,
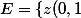Soient, \frac{|1-z|}{1-|z|}\leq k\})
et )
une suite de nombres complexes telle que la série entière 
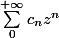
converge en z=1.
Notons
la somme de la série sur )
. Pour )
, développez }{1-z})
en séries entières.
La correction indique que en supposant la somme de la série nulle, on a:
}{1-z} =(\sum_n z^n)(\sum_n c_nz^n)=\sum_{p,q\eq 0}c_pz^{p+q}=\sum_n(\sum_{k=0}^nc_k)z^n)
Je comprends les dernières égalités mais pas la première, où est passé le)
au dénominateur ?
Soient
Notons
La correction indique que en supposant la somme de la série nulle, on a:
Je comprends les dernières égalités mais pas la première, où est passé le
Re: Développement en série entière
par capitaine nuggets » 16 Mai 2018, 11:38
Salut !
Pour tout
, 
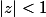
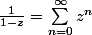
(série géométrique).
Pour tout
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :