Développement limité d'une suite récurrente

[Charmander]

Bonjour,

Soit pour n dans N.
1) Trouver un équivalent de
2) Trouver un équivalent de

En considérant j'ai montré que était équivalent à -1/n mais je n'arrive pas à trouver la question 2. J'ai posé puis j'ai considéré mais j'ai pas l'impression que ça me permette de conclure... Voyez-vous une méthode pour résoudre cet exercice ? Merci.

[Ben314]

Salut,
Je sais pas comment tu as fait pour la question 1).
Perso, (j'aime pas les négatifs et je vois mieux les truc en +oo), j'aurais posé ce qui donne :
et donc
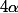
On en déduit (récurrence) que, pour tout n, , on en déduit que puis, que où est une constante.
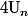
On réinjecte cette majoration dans la somme de (*) pour en déduire un minorant de contenant une somme qu'on évalue (ou minore) de nouveau à l'aide d'une comparaison somme/intégrale.
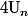
Je pense qu'à ce point, on a un encadrement suffisamment "fin" de pour répondre aux deux questions.