Bonjour,
Voici la question qui me pose problème :
Soit f l’application de deux variables définie par f(x, y) = ln(y − x^2) + x.
En déduire le développement limité à l’ordre 2 de f au voisinage de (0, 1).
Indication: On donne pour u voisin de 0 :
ln(1 + u) = u −(u^2/2) + . . . + [(−1)^(n+1). u^n/n ]+ o(un)
Dans une autre question j'ai trouvé le développement à l'aide de la formule de Taylor, je n'arrive pas à le retrouver avec cette autre formule.
En attente d'un peu d'aide, merci d'avance !
Développement limité
8 messages
- Page 1 sur 1
Re: Développement limité
Bonsoir,
J'ai trouvé le résultat avec la formule de Taylor mais je dois le retrouver par une autre méthode :
Indication: On donne pour u voisin de 0 :
ln(1 + u) = u −(u^2/2) + . . . + [(−1)^(n+1). u^n/n ]+ o(un)
C'est avec cette méthode que je ne vois pas comment m'y prendre.
J'ai trouvé le résultat avec la formule de Taylor mais je dois le retrouver par une autre méthode :
Indication: On donne pour u voisin de 0 :
ln(1 + u) = u −(u^2/2) + . . . + [(−1)^(n+1). u^n/n ]+ o(un)
C'est avec cette méthode que je ne vois pas comment m'y prendre.
Re: Développement limité
pour (x;y) voisin de (0;1)
h,k deux accroissements réels "petits"
=ln(1+k-h^2)+h)
on développe le logarithme:
=u-\frac{1}{2}u^2+o(u^2))
posons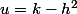
=k-h^2-\frac{1}{2}(k-h^2)^2+h+o(h^2+k^2))
=h+k-h^2-\frac{1}{2}k^2+o(h^2+k^2))
les termes de degré 3 de (k-h^2)^2 passent dans le petit o.
h,k deux accroissements réels "petits"
on développe le logarithme:
posons
les termes de degré 3 de (k-h^2)^2 passent dans le petit o.
Re: Développement limité
à noter que le DL avec le DL du log est bien plus rapide que le DL de Taylor avec le calcul de la différentielle et des termes d'ordre 2
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
