Dévellopement limité

[Ncdk]

Bonjour,

J'avais deux développement limité dans mes révisions dont j'ai pas la correction et je voudrais savoir si je me trompe ou pas.

1) à l'ordre n=4

J'ai fais un développement limité avec

J'ai donc posé pour retrouver donc

Le changement de variable est-il correcte ?

Car je suis dans l'embarrat, mon prof lui à posé en utilisant ... Je ne comprends pas pourquoi, à la fin il trouve que et moi je trouve

Qui a raison et qui à tort ?

2) à l'ordre n=13

Je fais d'abord le DL de et ensuite je fais une puissance partout ?

Je vois pas commencer procéder.

[zygomatique]

salut

si ton prof pose u = -x - x^2 alors il utilise le dl de 1/(1 + u) = 1/(1 - (-u)) !!!

[eratos]

salut

si ton prof pose u = -x - x^2 alors il utilise le dl de 1/(1 + u) = 1/(1 - (-u)) !!!

ce qui est plus astucieux :zen:

[Ncdk]

Bien vu, mais pourquoi on ne retombe pas sur la même chose, car ça revient au même non ? :triste:

[eratos]

Bien vu, mais pourquoi on ne retombe pas sur la même chose, car ça revient au même non ? :triste:

bah oui mais faut être rigoureux dans les calculs, il se peut que ton prof se trompe, mais plus souvent c'est l'élève :lol3:

Mais ça me chiffonne aussi, les termes en x² et x^3 devrait être là au final

[Ncdk]

bah oui mais faut être rigoureux dans les calculs, il se peut que ton prof se trompe, mais plus souvent c'est l'élève :lol3:

Je vais développer alors pour savoir si je me trompe.

Donc comme U=x+x²

J'obtiens :



Donc maintenant


Je ne tombe pas comme mon prof, je vois pas ou je fais faux du coup.

[eratos]

Je vais développer alors pour savoir si je me trompe.

Donc comme U=x+x²

J'obtiens :



Donc maintenant


Je ne tombe pas comme mon prof, je vois pas ou je fais faux du coup.

Logiquement, ton prof a tort: dans les termes ax bx² et cx^3 , a b et c snt non nuls car sommes d'entiers positifs stricts. Ces termes devraient donc persister dans l'équation finale.

[zygomatique]

dis à ton prof que c'est un bon à rien mauvais en tout .... :ptdr:

[Ncdk]

Je me disais bien qu'il y avait un soucis, merci :)

Pour le petit 2) d'ailleurs, quelqu'un peut m'aiguiller ? :)

[eratos]

Je me disais bien qu'il y avait un soucis, merci

Pour le petit 2) d'ailleurs, quelqu'un peut m'aiguiller ?

tu fais un Dl de sin, t'auras sin(u)=u-u^3/6+...=u(1-u²/6+....) puis tu utilises le dl usuel de (1+U)^a où U=-u²/6+...
Ca a l'air de marcher, après il y a peut etre des trucs plus ingénieux à faire.

[Ncdk]

tu fais un Dl de sin, t'auras sin(u)=u-u^3/6+...=u(1-u²/6+....) puis tu utilises le dl usuel de (1+U)^a où U=-u²/6+...
Ca a l'air de marcher, après il y a peut etre des trucs plus ingénieux à faire.

Super merci j'ai pu trouvé

J'avais une autre question me trotte dans l'esprit, à savoir qu'au niveau des DL, il arrive parfois que je trouve pas pareil que le prof en appliquant bêtement les formules, mais quand je trace les courbes à la calculette pour voir un ce qui se passe quand x tend vers 0 et la courbe du prof est parfaite limite alors que la mienne autour de 0 ça marche mais pourquoi nos résultats sont différent, pourtant un DL est pas unique ?

L'exemple en question :

à l'ordre 4

Version du prof :

on a le DL de cos(x) :

Donc après :




Ma version :

on a le DL de cos(x) :

Je sais aussi que

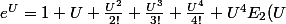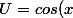Je pose puis après bah c'est de l'application toute bête, les puissances supérieures à 4 sont mis dans un E(x) et j'obtiens :




Je suis dans une impasse, je sais pas qui a raison et qui a tort, mais vu que quand je trace les fonctions trouvé avec , celle de mon prof imite bien la courbe autour de 0 et moi elle imite moins bien je trouve mais elle est limite confondu autour de 0 aussi, alors je sais pas si on peut avoir plusieurs DL différent...