Dev. en Série de Laurent
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Fløw
- Membre Naturel
- Messages: 24
- Enregistré le: 11 Nov 2010, 20:13
-
 par Fløw » 11 Nov 2010, 20:24
par Fløw » 11 Nov 2010, 20:24
Bonjour,
J'ai un exercice à travailler pour réviser un DS :
Il s'agit d'un simple développement en série de Laurent de la fonction suivante :
f(z) = (1+z)sin(z²)/(z^5)
Je suis donc parti sur la développement centré sur la singularité z=0 (qui est l'unique singularité , pôle d'ordre 5 si je ne me trompe pas). J'ai donc développé sin(z²) avec une série de taylor. Bref, à la fin j'obtiens f(z) = Somme de n = 0 à n [(-1)^n * (z^(4n)*((z+1)/((z^3)*(2n+1)!))] (Je sais pas comment la formule

pour que vous voyez bien)
Je voulais donc savoir comment exprimer la formule sous la forme de f(z) = Somme(An*(z-a)^n) avec a = 0 et An =
ça ou alors si mon expression actuelle suffisait pour dire que c'est un développement en série de Laurent...
Merci d'avance
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 11 Nov 2010, 22:00
par girdav » 11 Nov 2010, 22:00
Bonjour,
on effectue un développement en série entière au voisinage de

de
\sin (z^2))
, ensuite il suffira de diviser par
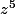
. Je crois que pour donner le coefficient

de ce développement en série il faudra regarder le reste de

modulo

.
-
Fløw
- Membre Naturel
- Messages: 24
- Enregistré le: 11 Nov 2010, 20:13
-
 par Fløw » 11 Nov 2010, 22:19
par Fløw » 11 Nov 2010, 22:19
Je vais regardé ça. . . mais ça revient à ce que j'ai fais il me semble.
(Question : Comment on fait sur ce forum pour écrire les formules comme tu viens de le faire ?)
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 11 Nov 2010, 22:22
par girdav » 11 Nov 2010, 22:22
Fløw a écrit:Je vais regardé ça. . . mais ça revient à ce que j'ai fais il me semble.
Oui, c'est juste qu'il faut regrouper les termes et c'est assez fastidieux, mais pas difficile.
Pour les formules, il faut mettre des balises TEX.
Les détails sont ici.
-
Fløw
- Membre Naturel
- Messages: 24
- Enregistré le: 11 Nov 2010, 20:13
-
 par Fløw » 11 Nov 2010, 22:27
par Fløw » 11 Nov 2010, 22:27
Alors, j'arrive à ce niveau là :
^{n} \frac{(z^{4n-2}+z^{4n-3})}{(2n+1)!})
Une fois arrivé là, j'avoue sécher totalement, que veux-tu dire par reste du modulo et regrouper les termes ?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 11 Nov 2010, 22:33
par girdav » 11 Nov 2010, 22:33
Je crois qu'il y a une coquille : la somme va de
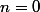
jusqu'à l'infini.
On veut un truc de la forme
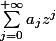
(pour la série entière). On peut couper la somme en deux : pour les indices

pairs et les indices

impairs (licite car la série est absolument convergente.
-
Fløw
- Membre Naturel
- Messages: 24
- Enregistré le: 11 Nov 2010, 20:13
-
 par Fløw » 11 Nov 2010, 22:45
par Fløw » 11 Nov 2010, 22:45
:hum:
Je développe, je sépare les termes paires et les termes impairs, mais j'avoue ne pas voir cette forme dont tu parles
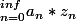
.... Je tourne en rond totalement :mur: :

-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 11 Nov 2010, 22:50
par girdav » 11 Nov 2010, 22:50
En fait je ne sais pas si on pourra trouver une jolie formule pour

(*), mais par exemple (je vais dire des âneries si on considère que c'est en rapport avec le problème en question)
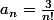
si

est congru à

modulo

,
!})
si

est congru à

modulo

, etc..
(*) quoique l'on peut "tricher", par exemple pour dire que l'on a
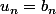
si

pair et
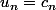
si

impair on peut écrire que
^n}2b_n+\frac{1-(-1)^n}2c_n)
.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 11 Nov 2010, 23:11
par Ben314 » 11 Nov 2010, 23:11
Ce que te dit Girdav, c'est uniquement que l'on peut écrire :
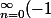^{n} \frac{(z^{4n-2}+z^{4n-3})}{(2n+1)!}<br />\ =\ \bigsum_{n=0}^{\infty} \frac{(-1)^{n}}{(2n+1)!}z^{4n-2}\ +\ <br />\bigsum_{n=0}^{\infty} \frac{(-1)^{n}}{(2n+1)!}z^{4n-3}\ =\ <br />\bigsum_{k=-3}^{\infty} a_kz^k)
où
^{n}}{(2n+1)!})
lorsque
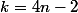
ou

et

sinon.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Fløw
- Membre Naturel
- Messages: 24
- Enregistré le: 11 Nov 2010, 20:13
-
 par Fløw » 11 Nov 2010, 23:18
par Fløw » 11 Nov 2010, 23:18
J'venais de saisir à l'instant...le temps de gratter sur papier et paf :) Merci beaucoup....Me manquait quelques nuances au niveau des congruences...ça manque de pas avoir fait spé maths de temps en temps ;) on oublie quelques notions. . . .Désolé pour les questions aux réponses triviales :o
MERCI :)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
