Détermination du logarithme

[Pafapafadidel]

Bonjour!

Je viens de résoudre un petit probleme, mais comme je ne suis pas sûr de mes notions, j'aimerais qu'on me confirme le résultat (ce qui du même coup confirmerait mes notions).

Soit a et b , a>0 et b>0. On s'intéresse aux solutions dans de l'équation .
Selon la détermination du logarithme que l'on choisit, il existe 3 ensembles de solutions possibles:
-
-
-

Qu'en pensez vous?

[Ben314]

Bonsoir,
Je pense qu'avec a>0 et z dans C, on a un peu du mal à définir ...
Comment le définit tu ?

[Ben314]

En relisant un peu mieux ton post, je me rend compte que tu as bien vu qu'il y avait un p.b. dans la définition du .
Le problème, je pense, c'est qu'il faut absolument dire comment tu définit avant ne serait ce que d'écrire ton équation, et donc bien avant de commencer à la résoudre.
Tu peut effectivement obtenir ou (ou d'autres...) ensembles de solutions selon la définition que tu prend de

Tu peut aussi obtenir un ensemble du type si tu définit "comme au colège" et donc uniquement pour z entier (mais, danc ce cas, ce n'est plus la peine de sortir les complexes pour résoudre l'équation)

[Pafapafadidel]

Je sais bien que le problème est un peu posé à l'envers, mais ma question porte justement sur ses solutions selon comment on le définit. Je m'explique:

. Si je ne m'abuse, avec la détermination principale du logarithme, n'a pas de sens pour a>0, donc l'ensemble de solution est , car on ne peut que parler de z entier. Si on prend une autre détermination du logarithme, l'ensemble de solution est soit soit selon si on enlève la demi-droite passant par avec ou celle passant par avec . Voilà mon raisonnement (qui peut être faux car je ne suis pas à l'aise avec le logarithme complexe, d'où ma question).

Tu as l'air de dire qu'on peut obtenir d'autres ensembles de solutions. Lesquels? Selon quelle façon de définir ?

[Ben314]

Pour moi, dans ce genre d'exo, on doit commencer par écrire :
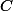
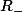
Je fixe une détermination du Log surprivé d'une demi-droite qui n'est pas la demi droite , puis, pour tout réel a>0, je pose .
Ensuite, tu peut "résoudre"....
En fonction de la détermination du Log choisie, on peut avoir
ou bien , mais aussi ou etc...
C'est pour cela que l'ensemble des solutions peut être ou ou.... d'autres ensembles....

P.S. Pour moi, UNE détermination du Log c'est UNE fonction telle que exp(Log(z))=z pour tout z dans le domaine de définition du Log.
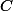
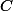
On peut montrer (et c'est TRES IMPORTANT) qu'il n'existe pas de détermination du Log sur privé de 0 mais qu'il en existe sur privé d'une demi droite d'origine 0. De plus, sur un tel domaine, il existe plusieurs déterminations du Log (on peut ajouter à une determination du Log, cela reste une détermination du Log).
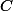
A noter que l'on peut aussi trouver des déterminations du Log sur des ensemble autres que privé d'une demi droite...

[Pafapafadidel]

Mon objectif est d'étudier les différentes déterminations du logarithme, c'est pourquoi j'ai écrit cela ainsi. Apres je comprends bien que ma formulation est suspecte et ambigue (mais vu que je me suis posé cet exercice moi même, j'ai pris quelques libertés).

Si je comprends bien, cela ne pose donc pas de problemes si la détermination du Log que l'on choisit ne prolonge pas le logarithme réel tant que l'on a exp(Log(z))=z.
Il est intéressant de noter que l'on retrouve les solution entieres usuelles (celles de college comme tu dis) en utilisant les bonnes déterminations du Log pour résoudre cette équation.

Tu as éclairé quelques points obscurs de mes connaissances en analyse complexe, Merci a toi!