Un déterminant

par **leon1789** » 18 Fév 2009, 21:02

Bonsoir,

Voici un déterminant polynomial qui m'intéresse :

Soit un polynôme

.
Pour un entier

, on considère le déterminant

de la matrice de

suivante :

C'est une matrice (k lignes , k colonnes) presque triangulaire inférieure mais avec des P ... P en première ligne.

Les entiers n et k sont indépendants.

Je sais que

où Q est un polynôme de degré au plus n-1 mais je n'arrive pas le prouver... :triste: Evidemment, je vois bien d'où sort le terme

, mais pour ce qui est du reste

, là, je suis sec : j'ai essayé une récurrence sur l'entier k, sur l'entier n, des bidouilles sur les lignes... Je n'y arrive pas.

Avez-vous des idées ? Merci pour vos réponses éventuelles.

par **R.C.** » 18 Fév 2009, 23:12

Bonsoir,

Je n'ai pas fait tous les calculs, mais j'ai fortement l'impression qu'en factorisant la première ligne par P, la seconde par X^(n-1), la troisième par X^(n-2) etc, tu te retrouve avec un déterminant dont la première colonne n'a que des polynômes de degré 0, la seconde de degré 1, etc.. Donc en comptant un peu tu te retrouve avec
P X^( (n-1) + (n-2) + .. + (n-k+1)) x R
où R est divisible par X ^ ( 1 + 2 + .. + (k-2)).
Hop, on touille tout ça et :id:

par **leon1789** » 18 Fév 2009, 23:20

Ok, je vais essayer de re-touiller comme tu l'indiques : ça pourrait peut-être donner une partie du résultat...
Merci.

par **leon1789** » 18 Fév 2009, 23:26

Merci

R.C. a écrit:tu te retrouve avec un déterminant dont la première colonne n'a que des polynômes de degré 0, la seconde de degré 1, etc..

pour la première colonne ok, mais pas pour les autres colonnes à cause des 1 sur la première ligne.

par **R.C.** » 18 Fév 2009, 23:29

ah oui exact, mais ce n'est pas super grave (c'est pour ca que R est divisible par X ^ ( 1 + 2 + .. + (k-2)) et pas X ^ ( 1 + 2 + .. + (k-1)).

par **leon1789** » 18 Fév 2009, 23:30

leon1789 a écrit:pour la première colonne ok, mais pas pour les autres colonnes à cause des 1 sur la première ligne.

ok, on peut effectivement poursuivre en éliminant tous les 1 (sauf un) sur la première ligne en soustrayant la dernière colonnes à toutes les autres. Du coup, on peut factoriser par X^0 X^1 ...

par **leon1789** » 18 Fév 2009, 23:34

Merci ! Ca a l'air bon pour trouver le facteur

:we:

Il reste maintenant à montrer que Q est de degré au plus n-1 . :doh:

par **Lemniscate** » 18 Fév 2009, 23:43

Salut,

Alors moi j'ai essayé ceci :

On note (C_i) les colonnes de ta matrice.
Pour i entre 1 et k-1 tu faits

.
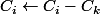
Donc tu te retrouves avec que des 0 dans la première ligne (sauf dans première ligne, dernière colonne, où tu as toujours P).

Tu fais un développement sur la dernière colonne, ce qui te donne un déterminant (k-1,k-1)

car que des 0 dans la première ligne ( (k-1) zéros donc) plus un déterminant (k-1,k-1) de la forme :

Après tu développes de proche en proche la dernière colonne, jusqu'à obtenir un déterminant carrée :

Je pense que cela peut être utile. Mais bon je suis pas sur...

EDIT : Le problème étant qu'il me manque le terme en

...

par **leon1789** » 18 Fév 2009, 23:58

Merci ! Je regarde ça tranquillement demain :id:

par **Lemniscate** » 19 Fév 2009, 00:08

En fait j'ai fait une petite (grosse) erreur, j'ai oublié des termes ! On aura toujours 2 termes dans la dernière colonne après les premier développement !!!

Donc je me repencherai plus tard sur ce problème, là je reste sec !

En tout cas je pense que le truc

pou

est utile,mais je crois que vous l'avez déjà vu !

Et l'idée de factorisation aussi est je le pense bonne.

Bonne chance, la nuit porte conseil.

par **leon1789** » 19 Fév 2009, 09:31

Lemniscate a écrit:En fait j'ai fait une petite (grosse) erreur, j'ai oublié des termes ! On aura toujours 2 termes dans la dernière colonne après les premier développement !!!

...mais ta manière de procéder montre quand même que le déterminant est multiple de

.

Le problème est maintenant de montrer que Q est de degré au plus n-1. Pour cela, je pense qu'il ne faut surtout pas factoriser par P, mais plutôt analyser les bonnes éliminations.

Lemniscate a écrit:Bonne chance, la nuit porte conseil.

Je dois dire que ça fait déjà plusieurs nuits que je suis dessus... :cry:

par **leon1789** » 19 Fév 2009, 10:50

Ah... comme souvent, le fait d'en parler débloque la situation.
Je crois que j'ai compris pourquoi degre(Q) <= n-1 : c'est une espèce de reste après une espèce de division polynomiale..

Merci à vous.

par **Lemniscate** » 19 Fév 2009, 16:29

Salut,

Je ne sais pas si ca peut te feire avancer mais peut-être que tu n'as pas encore pensé à écrire la formule brute du déterminant k x k ?

où

ensemble des permutations d'orde k,

la signature (+1 ou -1) de la permutaion

Peut-être que ca peut t'aider ???

par **leon1789** » 19 Fév 2009, 17:16

Maintenant, c'est bon : j'ai tout ce que je voulais :zen: ... pour trouver Q, il faut soustraire toutes les lignes à la première, puis développer le déterminant suivant la première ligne bien qu'il n'y ait aucun 0 (je n'y avais pas pensé avant car je ne suis pas masochiste ! mais en fait ça marche comme ça apparemment), puis on regarde les degrés des termes du développement...

Merci à vous.

par **Lemniscate** » 19 Fév 2009, 17:33

Effectivement je n'y aurais pas pensé de suite !

Donc si je comprend bien le premier terme du développement donne

et les autres trmes du développement donnent

?

par **leon1789** » 19 Fév 2009, 17:49

Lemniscate a écrit:Effectivement je n'y aurais pas pensé de suite !

Donc si je comprend bien le premier terme du développement donne et les autres trmes du développement donnent ?

Le premier terme se scinde en deux :

d'une part, et un petit bout de

d'autre part.
Et oui, les autres termes du développement fournissent aussi des bouts de

.

Un déterminant

un déterminant

Qui est en ligne