Déterminant matrice ayant tous ces coefs égaux sauf sur sa diagonale

[lirabo]

Voila,

J'ai M une matrice
Mii =a et Mij=b pour i!=j
donc mm valeur pour coef de la diagonale et mm valeur pour tous les autres coefs.
Je cherche son déterminant.

Je ne sais pas s'il existe une formule simple. Et si oui, comment elle se démontre (les grandes lignes suffiront)


Merci bcp !!

[majin]

Et si tu ajoutais à la première ligne toutes les autres?

[lirabo]

Et si tu ajoutais à la première ligne toutes les autres?

Hummm et ensuite ... ?

[wserdx]

Je te propose deux méthodes:
1 - démonstration par récurrence sur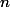 , taille des matrices, en essayant de deviner une formule pour . Pour la récurrence, retirer la première ligne multipliée par à toutes les autres, calculer le déterminant en développant par rapport à la première colonne.

2 - méthode plus directe: Soit la matrice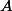 dont tous les coefficients sont . Elle est de rang 1, ces valeurs propres sont donc de multiplicité et de multiplicité .
Son polynôme caractéristique est donc

Je te laisse deviner ce que vaut

[lirabo]

Merci. La méthode 2 est très astucieuse.

Juste un détail : comment retrouves-tu la valeur propre de la matrice toute à a ?
Il me semble me souvenir qu'on peut appliquer l'opération inverse sur les colonnes à l'opération sur les lignes et que sans ce cas, on conserve les valeurs propres. Le but est alors de diagonaliser la matrice. Mais, ça n'a pas l'aire d'être ça...

[majin]

Hummm et ensuite ... ?

Bon je te propose ma méthode plus simple et en faisant appel qu'aux opérations élémentaires:
-On ajoute à la première ligne les autres, et on factorise par (n-1)b+a
-On que des 1 dans la première ligne, donc on soustrais la première ligne des autres
-On a alors une matrice diagonale de termes a-b

[lirabo]

Merci. très simple en effet.
euh comme je suis assez léger en théorie des matrices.

Tu te bases sur le fait qu'on puisse ajouter une ligne à une autre sans changer le déterminant
et
que le déterminant d'une matrice triangulaire estr le produit des coef de sa diagonale
?

[alm]

Salut

Une autre démarche:

Pour tout , on pose :
[CENTER][/CENTER]

1) On suppose que tel qu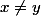e fixé.
Prouver que pour tout on a où et sont des constantes ne dépendant que de et .
2) Expliciter et en fonction de et (On pourra remarquer que pour 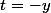(rep 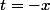) on obtient des matrices triangulaires superieure(resp. inférieure) )
3) En déduire une expression explicite de pour tout tel que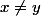
4) Soit . Pour tout , on pose . Calculer : . Que peut on en déduire ?