Déterminant à déterminer

par **megurine_luka** » 25 Sep 2010, 20:45

Bonsoir,

J'aimerais calculer ce déterminant, mais je ne vois pas trop comment faire.

MERCI BIEN

Bonne fin de soirée.

par **ffpower** » 25 Sep 2010, 21:03

Je suppose que tu veux dire "autrement qu'en faisant un calcul bourrin"..
Donc si on note M ta matrice, et A la matrice de permutation

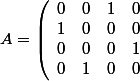alors on a

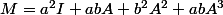
, donc un calcul des valeurs propres de A donnera les valeurs propres de M, et donc son déterminant..

par **megurine_luka** » 25 Sep 2010, 21:12

Je ne connais pas encore les valeurs propres y a t-il un moyen de calculer le déterminant sans calcul bourrin ni valeurs propres?

par **ffpower** » 25 Sep 2010, 21:15

Ah dans ce cas je passe mon tour. Je vois pas de simplification évidente par opérations sur lignes/colonnes en tout cas..

par **girdav** » 26 Sep 2010, 13:13

Bonjour,
on peut commencer par faire

, sortir

, puis

,

et

.
Je trouve au final que le déterminant vaut

, ce qui semble cohérent puisqu'il est homogène de degré

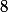
et est nul pour

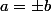
. Mais ceci ne prouve pas que c'est correct et le meilleur moyen de le savoir est évidemment de mener à bien le calcul.

par **megurine_luka** » 26 Sep 2010, 13:31

ensuite je factorise?

par **girdav** » 26 Sep 2010, 13:33

En fait tu as fait des combinaisons sur les colonnes alors que je proposait de les faire sur les lignes. Mais on peut rebondir en remplaçant dans mon premier message la lettre L par la lettre C, et donc continuer à manipuler des colonnes.

par **megurine_luka** » 26 Sep 2010, 13:42

donc j'ai
l1<-l1+l2+l3+l4

ensuite je fais

l2<-l2-l3

ensuite comment je fais? :triste:

par **girdav** » 26 Sep 2010, 13:46

megurine_luka a écrit:donc j'ai
l1<-l1+l2+l3+l4

En fait je me suis planté dans les combinaisons : ici il faut faire

,

et

.

par **megurine_luka** » 26 Sep 2010, 13:53

d'accord merci donc j'ai trouvé cela. Je continue comment?

par **girdav** » 26 Sep 2010, 13:56

Tu peux développer par rapport à la dernière colonne puis la première ligne. Et n'oublie pas le facteur

devant.

par **megurine_luka** » 26 Sep 2010, 14:03

=

est-ce ce qu'il faudrait faire?

par **girdav** » 26 Sep 2010, 14:04

Oui, maintenant tu peux développer par rapport à la première ligne.

par **megurine_luka** » 26 Sep 2010, 14:10

=

j'ai plus qu'à développer?

par **girdav** » 26 Sep 2010, 14:14

Non la stratégie est d'obtenir un truc factorisé. On peut s'aider du fait que

.

par **megurine_luka** » 26 Sep 2010, 14:27

ah effectivement
Merci beaucoup cela donne bien

Merci encore

Déterminant à déterminer

déterminant à déterminer

Qui est en ligne