Détection d'identité remarquable

[Lioooon]

Salut,
√de 3 - 2√2 (LA RACINE COMPORTE TOUT: 3 - 2√2) = √2 + 1 - 2√2 (PAREIL) = √(√2 - 1)^2 (PAREIL)= √2 - 1 (LÀ c'est juste le 2)
Comment on passe de la 2ème à la 3ème étape?
merci d'avance

[Ben314]

Bon, déjà, si tu veut que quelqu'un s'interesse à tes question, tu ferait plus que bien de te mettre au MimeTeX : lycee/ecrire-des-belles-formules-mathematiques-balises-tex-t70548.html
Là, il faut déjà 5 bonnes minutes pour comprendre ce que tu écrit et encore avec de gros doutes sur le sens...

[Ben314]

Sinon, après "décryptage", il semblerais que ta question soit
"Comment montre t-on que ?"
ce qui n'a clairement rien a faire dans "supérieur" vu que c'est au collège qu'on apprend que .

Si la question est "Comment fait-on pour se rendre compte que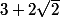 est un carré "simple" ?" alors la réponse est :
Il est évident que le carré d'un nombre de la forme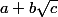 (avec a,b,c entiers, voire rationnels) est lui aussi de cette forme là donc quand on a du , on "teste" pour voir si par hasard ça ne s'écrirait pas 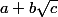(des fois ça marche, mais pas toujours...)
Des fois, c'est même plus vicieux, par exemple peut éventuellement s'écrire vu que le carré de est bien de la forme

[Lioooon]

je trouve (√2+1)^2
je ne comprends pas d'où vient le moins

[Ben314]

Ma calculette me donne alors que ...

[Lioooon]

lil oui mais tu peux me dire à qui il appartient ce moins. Je ne comprends pas

[Sake]

lil oui mais tu peux me dire à qui il appartient ce moins. Je ne comprends pas

Développe simplement et reviens nous dire ce que ça donne...

[Lioooon]

ok ça fait bien 2 + 1 - 2√2 MAIS comment tu fait pour voir au premier coup d'oeil que c'est -1? Juste parce que c'est - 2√2?

[Ben314]

Déjà, je ne risque pas "de voir du premier coup que le - provient du -1" vu qu'il est évident que (car ) donc le moins tu le met ou tu veut.
Ensuite, a mon époque, on voyait au collège que l'identité "remarquable" devenait, si on remplaçait b par -b (ou a par -a) .

[Lioooon]

ok merci

[Sake]

ok merci

Comme te le dit Ben314, ça requiert avant tout de l'entraînement. Si tu ne t'habitues pas à factoriser ces expressions polynomiales en utilisant la forme canonique, tu n'acquerras jamais ce réflexe.