Détection de Collision entre Tétraèdre
15 messages
- Page 1 sur 1
Détection de Collision entre Tétraèdre
Bonjour,
Je suis élève en 1ère année de prépa et je cherche une formule ou un test qui permet de savoir si deux tétraèdres sont enchevétrés l'un dans l'autre ? ou bien à détecter si une face est enchevétrés dans une autre ?
Si quelqu'un sait résoudre cette énigme pour moi, je le remerci par avance.
:we:
Je suis élève en 1ère année de prépa et je cherche une formule ou un test qui permet de savoir si deux tétraèdres sont enchevétrés l'un dans l'autre ? ou bien à détecter si une face est enchevétrés dans une autre ?
Si quelqu'un sait résoudre cette énigme pour moi, je le remerci par avance.
:we:
leolio a écrit:Bonjour,
Je suis élève en 1ère année de prépa et je cherche une formule ou un test qui permet de savoir si deux tétraèdres sont enchevétrés l'un dans l'autre ? ou bien à détecter si une face est enchevétrés dans une autre ?
Si quelqu'un sait résoudre cette énigme pour moi, je le remerci par avance.
:we:
Ba l'equation de ton tetraedre dans l'espace, est composé des equations des quatres plans qui la compose(normalement tu as au sein meme d'un plan les condition liant deux variables pour delimiter les contours du triangle).
Si deux plans des deux tetraedres ont la meme equation, c'est que les tetraedres ont une face commune.
qu'est-ce que tu attend comme réponse à tes questions ?
- s'il existe un test pour dire si deux tétraèdres sont d'intersection
non vide ? oui
- comment déterminer ce test ?
par exemple, considérer les tétraèdres comme enveloppes convexes
de leurs quatre sommets, puis exprimer en coordonnées barycentriques
le fait que leur intersection est non vide
- faire les calculs ?
- les programmer ?
- s'il existe un test pour dire si deux tétraèdres sont d'intersection
non vide ? oui
- comment déterminer ce test ?
par exemple, considérer les tétraèdres comme enveloppes convexes
de leurs quatre sommets, puis exprimer en coordonnées barycentriques
le fait que leur intersection est non vide
- faire les calculs ?
- les programmer ?
Non, je ne cherche pas à savoir si mes tétraèdres ont une face commune ou pas, cela serait trivial et je n aurai donc pas posé la question.
Si un premier tétraèdre est constitué des coordonnées suivantes :
A = (0,0,0)
B = (2,0,0)
C = (1,2,0)
D = (5.1.2)
et le second avec les coordonnées suivantes :
A = (4,0,0)
B = (6,0,0)
C = (5,2,0)
D = (1.1.2)
Je cherche vraiment à déterminer par un test ou une équation que je dois programmer si deux tétraèdres sont enchevétrés l'un dans l'autre, forme inaproprié pour ce que je cherche à faire.
Merci d'avance à celui qui résout cette enigme.
Si un premier tétraèdre est constitué des coordonnées suivantes :
A = (0,0,0)
B = (2,0,0)
C = (1,2,0)
D = (5.1.2)
et le second avec les coordonnées suivantes :
A = (4,0,0)
B = (6,0,0)
C = (5,2,0)
D = (1.1.2)
Je cherche vraiment à déterminer par un test ou une équation que je dois programmer si deux tétraèdres sont enchevétrés l'un dans l'autre, forme inaproprié pour ce que je cherche à faire.
Merci d'avance à celui qui résout cette enigme.
si l'on programme de façon bourrine:
on considère le 1er tétraèdre ABCD.
avec)
idem pour les points B,C,D.
Ensuite, par exemple pour avoir l'équation du plan (ACD)
)
)
puis on calcule les coordonnées d'un vecteur normal au plan (ACD):
calcul des coordonnées de vectoriel
vectoriel  :
:
(z_{D}-z_{A})-(z_{C}-z_{A})(y_{D}-y_{A}))
(x_{D}-x_{A})-(x_{C}-x_{A})(z_{D}-z_{A}))
(y_{D}-y_{A})-(y_{C}-y_{A})(x_{D}-x_{A}))
puis équation du plan (ACD):
+\Delta_{2}(y-y_{A})+\Delta_{3}(z-z_{A})=0)
ensuite on teste le signe de cette application affine évaluée sur les coord. de B:
+\Delta_{2}(y_{B}-y_{A})+\Delta_{3}(z_{B}-z_{A}))
l' intérieur du tétraèdre est donnée par quatre équations dont la premiere
est donnée par:
 + \Delta_{2} (y-y_{A}) + \Delta_{3} (z-z_{A}) \right) > 0)
le tétraèdre est donnée par quatre équations dont la premiere
est donnée par:
 + \Delta_{2} (y-y_{A}) + \Delta_{3} (z-z_{A}) \right) \geq 0)
on considère le 1er tétraèdre ABCD.
avec
idem pour les points B,C,D.
Ensuite, par exemple pour avoir l'équation du plan (ACD)
puis on calcule les coordonnées d'un vecteur normal au plan (ACD):
calcul des coordonnées de
puis équation du plan (ACD):
ensuite on teste le signe de cette application affine évaluée sur les coord. de B:
l' intérieur du tétraèdre est donnée par quatre équations dont la premiere
est donnée par:
le tétraèdre est donnée par quatre équations dont la premiere
est donnée par:
soit  + \Delta_{2} (y-y_{A}) + \Delta_{3} (z-z_{A}) \right))
l'application affine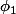 délimite trois régions de l'espace.
délimite trois régions de l'espace.
Comme il y a 4 applications affines de même forme que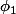
le tétraèdre ABCD détermine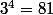 régions de l'espace.
régions de l'espace.
exemple d'une région:
 > 0) et
et  < 0) et
et  = 0)
Ensuite, on considère un deuxième tétraèdre quelconque EFGH:
il suffit de tester à quelles régions appartient E puis F puis G puis H.
ça fait donc 81^4 cas, soit
43046721 cas à tester au maximum !!
l'application affine
Comme il y a 4 applications affines de même forme que
le tétraèdre ABCD détermine
exemple d'une région:
Ensuite, on considère un deuxième tétraèdre quelconque EFGH:
il suffit de tester à quelles régions appartient E puis F puis G puis H.
ça fait donc 81^4 cas, soit
43046721 cas à tester au maximum !!
g une solution à proposer:
soient ABCD et EFGH deux tétraèdres quelconques (24 coordonnées).
principe de base: trois cas exclusifs sont possibles:
1) il y a une face de ABCD et une face de EFGH qui s'intersectent
2) ABCD et EFGH sont disjoints
3) l'un est inclu strictement dans l'autre
On va écrire une routine informatique pour tester le cas (1).
pour tester le cas (1).
 accepte en entrée 18 coordonnées, les coordonnées
accepte en entrée 18 coordonnées, les coordonnées
des six sommets ABC;EFG de deux triangles quelconques.
Lemme: si ABC est un triangle, tout point de son enveloppe convexe est obtenu comme barycentre à coefficients positifs de somme égale à 1, de A,B,C.
la routine teste si deux faces ABC et EFG ont au moins un
teste si deux faces ABC et EFG ont au moins un
point d'intersection:
on écrit donc cinq équations à 6 inconnues a,b,c,u,v,w:
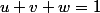
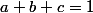



et six inégalités:

soient ABCD et EFGH deux tétraèdres quelconques (24 coordonnées).
principe de base: trois cas exclusifs sont possibles:
1) il y a une face de ABCD et une face de EFGH qui s'intersectent
2) ABCD et EFGH sont disjoints
3) l'un est inclu strictement dans l'autre
On va écrire une routine informatique
des six sommets ABC;EFG de deux triangles quelconques.
Lemme: si ABC est un triangle, tout point de son enveloppe convexe est obtenu comme barycentre à coefficients positifs de somme égale à 1, de A,B,C.
la routine
point d'intersection:
on écrit donc cinq équations à 6 inconnues a,b,c,u,v,w:
et six inégalités:
le systeme composé de cinq égalités et six inconnues et six inégalités
s'enrichit de deux nouvelles égalités. En effet
ABC sont coplanaires. Ecrivons l'équation normalisée de leur plan (ABC):
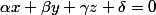
avec
En faisant des combinaisons linéaires d'égalités du système, il vient:
 + b \left( \alpha x_{F} + \beta y_{F} + \gamma z_{F} \right) + c \left( \alpha x_{G} + \beta y_{G} + \gamma z_{G} \right) = - \delta \left( u+v+w \right) = - \delta)
de même, EFG sont coplanaires:
Ecrivons l'équation normalisée de leur plan (EFG):

avec
il vient:
 + v \left( \epsilon x_{B} + \phi y_{B} + \chi z_{B} \right) + w \left( \epsilon x_{C} + \phi y_{C} + \chi z_{C} \right) = - \psi \left( a+b+c \right) = - \psi)
s'enrichit de deux nouvelles égalités. En effet
ABC sont coplanaires. Ecrivons l'équation normalisée de leur plan (ABC):
avec
En faisant des combinaisons linéaires d'égalités du système, il vient:
de même, EFG sont coplanaires:
Ecrivons l'équation normalisée de leur plan (EFG):
avec
il vient:
Les deux premières égalités permettent de se ramener à un système
à 4 inconnues a,b,u,v et cinq équations:
Il ne reste plus qu'à discuter ce système selon la méthode de Cramer.
La routine accepte donc en entrée six points ABC,EFG
accepte donc en entrée six points ABC,EFG
formant deux triangles et renvoie:
1 si ABC et EFG ont un point commun
0 si ABC et EFG sont d'intersection vide.
Ensuite; on ecrit un programme principal qui appelle
la routine avec les 16 couples de faces.
avec les 16 couples de faces.
ABC et EFG,
ABC et EFH,
ABD et FGH etc..
si la routine renvoie 1, les tétraèdres se chevauchent.
si la routine renvoie tjrs 0, les tétraèdres sont disjoints
ou inclus.
j'évalue ça à 300 lignes de code.
à 4 inconnues a,b,u,v et cinq équations:
Il ne reste plus qu'à discuter ce système selon la méthode de Cramer.
La routine
formant deux triangles et renvoie:
1 si ABC et EFG ont un point commun
0 si ABC et EFG sont d'intersection vide.
Ensuite; on ecrit un programme principal qui appelle
la routine
ABC et EFG,
ABC et EFH,
ABD et FGH etc..
si la routine renvoie 1, les tétraèdres se chevauchent.
si la routine renvoie tjrs 0, les tétraèdres sont disjoints
ou inclus.
j'évalue ça à 300 lignes de code.
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 76 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
