Dérivée d'une fonction.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Waru
- Messages: 2
- Enregistré le: 16 Jan 2008, 14:49
-
 par Waru » 16 Jan 2008, 15:02
par Waru » 16 Jan 2008, 15:02
Bonjour à tous,
je suis étudiant en régendat mathématique et dans le cadre de mon tfe sur les spirales, je suis amené à dériver la fonction suivante:

Mon problème est que d'une part, je n'arrive pas à isoler les y dans un des membres et d'autre part, je ne vois pas comment dériver une fonction pareille.
Pour l'information, si je ne me suis pas trompé, il s'agit de l'équation d'une spirale d'archimède en coordonnée cartésienne. Mon but est de trouver l'angle formé par la tangente en un point de la spirale et l'axe des abscisses.
Merci beaucoup de prendre la peine de lire ce message, et j'espère que vous pourrez me mettre sur la piste.
Bien à vous. =)
J.G.

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 16 Jan 2008, 21:16
par nuage » 16 Jan 2008, 21:16
Salut,
Waru a écrit:Mon problème est que d'une part, je n'arrive pas à isoler les y dans un des membres et d'autre part, je ne vois pas comment dériver une fonction pareille.
C'est normal : ce n'est pas une fonction.
Waru a écrit:Pour l'information, si je ne me suis pas trompé, il s'agit de l'équation d'une spirale d'archimède en coordonnée cartésienne. Mon but est de trouver l'angle formé par la tangente en un point de la spirale et l'axe des abscisses.
Pour ceci il vaut sans doute mieux utiliser une équation paramétrique de la spirale d'Archimède :

-
seriousme
- Membre Relatif
- Messages: 122
- Enregistré le: 26 Fév 2007, 13:10
-
 par seriousme » 16 Jan 2008, 21:56
par seriousme » 16 Jan 2008, 21:56
Si c'est une spirale les coordonnées polaires semblent bien adaptées .
L'équation devient alors :
 = \alpha\theta)
autrement dit la distance euclidienne à l'origine des points de la spirale croit linéairement avec l'angle de la rotation .
)\arccos(\frac{x}{\sqrt{x^2 + y^2}})<br />& \Longleftrightarrow & <br />\rho\sin(\theta) = \sin(\arccos(\frac{\rho\cos(\theta)}{\rho})) \arccos{\frac{\rho\cos(\theta)}{\rho}}\\<br />& \Longleftrightarrow &<br />\rho\sin(\theta) = \sin(\theta)\theta \\<br />& \Longleftrightarrow &<br />\rho = \theta\\<br />\end{eqnarray*})
Donc dans ce cas
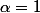
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités

