Salut,
En fait, vu ta définition de "C1 par morceaux", si tu prend la restriction de
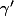
sur n'importe lequel des intervalles
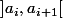
, tu obtient une fonction continue qui peut se prolonger par continuité aux deux extrémités de l'intervalle de façon à former une fonction continue sur l'intervalle
fermé 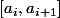
.
Ensuite, une fonction
continue sur un intervalle fermé borné, c'est forcément intégrable au sens de Riemann.
Et enfin, l'intégrale de
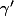
sur tout l'intervalle [a,b], c'est bien évidement la somme (finie) des intégrales sur chacun des
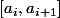
.
Bref, pour définir ce type d'intégrale, il n'est pas utile de connaître la théorie de Lebesgue et il n'y a même pas besoin de connaître grand chose à la théorie de Riemann : c'est des intégrales "style Lycée" où il n'y a pas le moindre problème de convergence de l'intégrale.
Sinon, et effectivement,
)
n'est pas bien définie : il y a en fait deux "valeurs" de la dérivée en

qui sont la limite à droite et la limite à gauche (que l'on note en général
)
et
)
).
Mais cette "indétermination" sur les valeurs des
)
ne change rien à la valeur de l'intégrale.
