Dérivée

[potter]

bonjour!
on me demande dans des exercices d'étudier la dérivabilité de fonctions
je dois donc faire toute une série de démonstrations pour voir si cette fonction est dérivable sur quel(s) intervalle(s) (lim quand h tend vers 0 de f(x°+h)-f(x°)/h pour certains points, compositions ...)
Pourquoi n'ai je pas tout simplement le droit de calculer f '(x) et de dire sur quel(s) intervalle(s) f est dérivable (par exemple si je vois qu'il y a une valeur interdite dans le résultat de f ' (x) je sais qu'elle n'est pas dérivable en ce point...c'est beaucoup plus rapide que de faire une démonstration avec lim quand h tend vers 0 de f(x°+h)-f(x°)/h !)
merci d'avance!

[echevaux]

Bonsoir

Applique ta méthode à :
la fonction f définie sur IR par f(x)=|x| est-elle dérivable en 0 ?

[potter]

effectivement :happy2: il n'y pas de formule pour la dérivée des valeurs absolus
mais pour des fonctions avec logarithmes, exponentielles, racines carrées je ne comprend pas pourquoi on me demande d'utiliser cette méthode longue...

[potter]

okay merci!
donc pour f(x)= x \sqrt {x}
je peux dire que f' (x)= sqrt {x} + x/sqrt {x} donc il me reste plus qu'à étudier la dérivabilité en 0...

[potter]

sqrt {x} représente racine de x

[potter]

exact!! x/Vx=Vx
mais dans ce cas là, si f(x)=xVx
f'(x)=2Vx donc, pas de valeurs interdites, et on peut dire que f est dérivable pour tout x supérieur ou égal à 0 , non?

[Black Jack]

okay merci!
donc pour f(x)= x \sqrt {x}
je peux dire que f' (x)= sqrt {x} + x/sqrt {x} donc il me reste plus qu'à étudier la dérivabilité en 0...

Sans me meler à la discussion sur la notion de dérivabilité d'une foncion.

L'expression de f '(x) que tu as écrite n'est pas correcte.

:zen:

[potter]

Comment calcules tu la dérivée de ????

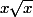
ah non dsl, je trouve 3/2 de racine de x
mais là encore je ne comprend pas pourquoi il faut utiliser la methode longue alors qu'il n'y a pas de valeurs interdites dans le resultat de f '(x)