Dérivée de polynome
21 messages
- Page 1 sur 2 - 1, 2
Dérivée de polynome
Bonjour, j'aimerais avoir de l'aide pour cet exercice de polynomes :
Au polynome P, on associe le polynome: Q_p(X)=(3X+8)P(X)+(X²-5X)P'(X)-(X^3-X²)P"(X)
1. Comparer, lorsque P est non nul, le degré de P et celui de Q_p
2. Que vaut P lorsque Q_p est le polynome nul?
3. Trouver les couples (a,P) où a est un nombre réel, P un polynome réel tels que Q_p=aP.
j'ai fait :
1. si P a pour degré1, alors Q_p a pour degré 2 donc si P a pour degré n alors Q_p aura pour degré n+1.
2. On résous : (3X+8)P(X)+(X²-5X)P'(X)-(X^3-X²)P"(X)=0
si je résonne sur les degrés, deg(P')=deg(P)-1 et deg(P")=deg(P)-2 donc : deg(3X+8)+deg(P)+deg(X²-5X)+deg(P)-1-deg(X^3-X²)-degP+2=0
deg(P)+1=0 donc deg(P)=-1 ??
étrange
merci de m'aider et notamment pour la c)
Au polynome P, on associe le polynome: Q_p(X)=(3X+8)P(X)+(X²-5X)P'(X)-(X^3-X²)P"(X)
1. Comparer, lorsque P est non nul, le degré de P et celui de Q_p
2. Que vaut P lorsque Q_p est le polynome nul?
3. Trouver les couples (a,P) où a est un nombre réel, P un polynome réel tels que Q_p=aP.
j'ai fait :
1. si P a pour degré1, alors Q_p a pour degré 2 donc si P a pour degré n alors Q_p aura pour degré n+1.
2. On résous : (3X+8)P(X)+(X²-5X)P'(X)-(X^3-X²)P"(X)=0
si je résonne sur les degrés, deg(P')=deg(P)-1 et deg(P")=deg(P)-2 donc : deg(3X+8)+deg(P)+deg(X²-5X)+deg(P)-1-deg(X^3-X²)-degP+2=0
deg(P)+1=0 donc deg(P)=-1 ??
étrange
merci de m'aider et notamment pour la c)
pluie2 a écrit:Bonjour, j'aimerais avoir de l'aide pour cet exercice de polynomes :
Au polynome P, on associe le polynome: Q_p(X)=(3X+8)P(X)+(X²-5X)P'(X)-(X^3-X²)P"(X)
1. Comparer, lorsque P est non nul, le degré de P et celui de Q_p
2. Que vaut P lorsque Q_p est le polynome nul?
3. Trouver les couples (a,P) où a est un nombre réel, P un polynome réel tels que Q_p=aP.
j'ai fait :
1. si P a pour degré1, alors Q_p a pour degré 2 donc si P a pour degré n alors Q_p aura pour degré n+1.
2. On résous : (3X+8)P(X)+(X²-5X)P'(X)-(X^3-X²)P"(X)=0
si je résonne sur les degrés, deg(P')=deg(P)-1 et deg(P")=deg(P)-2 donc : deg(3X+8)+deg(P)+deg(X²-5X)+deg(P)-1-deg(X^3-X²)-degP+2=0
deg(P)+1=0 donc deg(P)=-1 ??
étrange
merci de m'aider et notamment pour la c)
il faudrait d'abord verifier que le coefficient de X^(n+1) n'est pas nul
or il est égal à (n+1)(3-n)an
bonjour, si je comprends bien dans cette définition, il faut que je "choisisse" le plus grand degré des 3 et donc ensuite que je teste avec des degrés inférieurs à celui choisi ?
ici : deg(R+S+T) <=max{deg((R),deg((S),deg((T)}=deg(R3) mais le problème c'est que dg(P")=degP-2 donc comment faire pour trouver le max sans autres indications?
ici : deg(R+S+T) <=max{deg((R),deg((S),deg((T)}=deg(R3) mais le problème c'est que dg(P")=degP-2 donc comment faire pour trouver le max sans autres indications?
Bonjour.
On est à la question 2) où=0)
Même si on détermine le max des trois, on n'a pas l'égalité) =
=,\deg(S),\deg(T)\})
Il se trouve qu'ici \le n+1) car
car =\deg(R_2)=\deg(R_3) = n+1) .
.
En posant=\sum_{k=0}^na_nX^n, \quad a_n\ne 0) , les termes de plus degré de
, les termes de plus degré de =(3X+8)P(X), \quad R_2(X)=(X^2-5X)P'(X),\quad R_3(X)=(X^3-X^2)P''(X)) sont alors respectivement
sont alors respectivement a_nX^{n+1}) . On aura ainsi
. On aura ainsi a_n=a_n(3+n-n(n-1)=0) d'où
d'où =0) (
(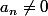) . Les degrés
. Les degrés  à chercher doivent vérifier l'équation
à chercher doivent vérifier l'équation =-n^2+2n+3=0) . Cette équation admet-elle des racines entières? En répondant à cette question, tu pourras déterminer les solutions de
. Cette équation admet-elle des racines entières? En répondant à cette question, tu pourras déterminer les solutions de 
pluie2 a écrit:bonjour, si je comprends bien dans cette définition, il faut que je "choisisse" le plus grand degré des 3 et donc ensuite que je teste avec des degrés inférieurs à celui choisi ?
ici : deg(R+S+T) <=max{deg((R),deg((S),deg((T)}=deg(R3) mais le problème c'est que dg(P")=degP-2 donc comment faire pour trouver le max sans autres indications?
On est à la question 2) où
Même si on détermine le max des trois, on n'a pas l'égalité
Il se trouve qu'ici
En posant
deltab a écrit:Bonjour.
On est à la question 2) où
Même si on détermine le max des trois, on n'a pas l'égalité=
Il se trouve qu'icicar
.
En posant, les termes de plus degré de
sont alors respectivement
. On aura ainsi
d'où
(
. Les degrés
à chercher doivent vérifier l'équation
. Cette équation admet-elle des racines entières? En répondant à cette question, tu pourras déterminer les solutions de
j'avais déjà indiqué ce résultat et donné la factorisation le 15 à 19h08
Bonjour.
Je suis entièrement d'accord mais tu as laissé passer l'erreur concernant le degré d'une somme ou différence de polynômes, ce qui est grave pour moi vu le résultat qu'il a donné, il a utilisé les 2 formules fausses deg(R+S)=deg(R)+deg(S), deg(R-S)=deg(R)-deg(S) et et dans ce sens que j'avais continué la discussion et étais amené à redonner ton résultat. C'est ton résultat et je n'en réclames pas la paternité
Manny06 a écrit:j'avais déjà indiqué ce résultat et donné la factorisation le 15 à 19h08
Je suis entièrement d'accord mais tu as laissé passer l'erreur concernant le degré d'une somme ou différence de polynômes, ce qui est grave pour moi vu le résultat qu'il a donné, il a utilisé les 2 formules fausses deg(R+S)=deg(R)+deg(S), deg(R-S)=deg(R)-deg(S) et et dans ce sens que j'avais continué la discussion et étais amené à redonner ton résultat. C'est ton résultat et je n'en réclames pas la paternité
deltab a écrit:Bonjour.
Je suis entièrement d'accord mais tu as laissé passer l'erreur concernant le degré d'une somme ou différence de polynômes, ce qui est grave pour moi vu le résultat qu'il a donné, il a utilisé les 2 formules fausses deg(R+S)=deg(R)+deg(S), deg(R-S)=deg(R)-deg(S) et et dans ce sens que j'avais continué la discussion et étais amené à redonner ton résultat. C'est ton résultat et je n'en réclames pas la paternité
pas de problème!!
Bonsoir.
1) n'est nulle part définie et n'est donc pas un polynôme, je peut interpréter (donc interprétation personnelle) Q comme une application de \matbb{R}[X] dans lui-même où on a posé
n'est nulle part définie et n'est donc pas un polynôme, je peut interpréter (donc interprétation personnelle) Q comme une application de \matbb{R}[X] dans lui-même où on a posé =Q_P) , c'est
, c'est  qui est un polynôme.
qui est un polynôme.
2) On avait posé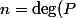) , ce n'est pas
, ce n'est pas  (<=n+1))
3) On est arrivé à la condition nécessaire (mais non suffisante)=3) . Il reste à trouver parmi les polynômes de degré 3 ceux qui sont effectivement solutions de
. Il reste à trouver parmi les polynômes de degré 3 ceux qui sont effectivement solutions de  . On procède par la méthode des coefficients indéterminés pour trouver P(X) donc poser
. On procède par la méthode des coefficients indéterminés pour trouver P(X) donc poser =aX^3+bX^2+cX+d) , etc .............................
, etc .............................
pluie2 a écrit:oui les racines sont 3 et -1 donc le degré de Q est de degré 3 nécessairement?
1)
2) On avait posé
3) On est arrivé à la condition nécessaire (mais non suffisante)
Bonjour.
Quand on a posé=aX^3+bX^2+cX+d) ,
, 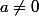 . Le fait que tu trouves a=0 prouve que tu as fait des erreurs de calculs quelque part, il fallait refaire le calcul de Q_P(X).
. Le fait que tu trouves a=0 prouve que tu as fait des erreurs de calculs quelque part, il fallait refaire le calcul de Q_P(X).
Si=2ax^3+4cx^2+(3d+3c)x+8d=0) , pourquoi tu identifies
, pourquoi tu identifies  à
à  alors qu'il fallait l'identifier au polynôme nul.
alors qu'il fallait l'identifier au polynôme nul.
pluie2 a écrit:je trouve ceci après développement :
2ax^3+4cx²+(3d+3c)x+8d=0
par identification, je trouve : 2a=a ; 4c-b=0;3d+2c=0 et 8d=d donc a=0 d=0c=0 et b=0??
c'est impossible où ai je pu me tromper? dans le système?
Quand on a posé
Si
21 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
