Dérivée matricielle
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 04 Déc 2014, 10:09
par Dante0 » 04 Déc 2014, 10:09
Bonjour,
Je ne comprends pas la résolution de cette dérivée :
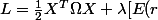-X^TR] + \gamma(1-X^T\bar{1}))
Je cherche

et je trouve

Je ne comprends pas d'ou vient la première partie à savoir le

? Ou est passé le 1/2 ? et le
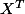
?
Sachant que X est une matrice
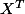
sa transposée, omega étant la matrice de variance covariance.
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 04 Déc 2014, 10:32
par arnaud32 » 04 Déc 2014, 10:32
ecris la definition
je suppose que Omega est symetrique non?
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 04 Déc 2014, 10:39
par Dante0 » 04 Déc 2014, 10:39
arnaud32 a écrit:ecris la definition
je suppose que Omega est symetrique non?
La définition de ? :hein:
Oui elle est symétrique !
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 04 Déc 2014, 11:12
par arnaud32 » 04 Déc 2014, 11:12
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 04 Déc 2014, 11:15
par Dante0 » 04 Déc 2014, 11:15
arnaud32 a écrit: - L(X) =\\<br /> \frac{1}{2}( H^T \Omega X+X^T \Omega H)+\frac{1}{2}( + H^T \Omega H) -\lambda H^TR - \gamma .H^T\bar{1}\\<br />= H^T \Omega X -\lambda H^TR - \gamma .H^T\bar{1} +\frac{1}{2}( H^T \Omega H)\\<br />= H^T .(\Omega X -\lambda R - \gamma .\bar{1}) +\frac{1}{2}( H^T \Omega H))
Euh... qu'est-ce que c'est ? :doh: :hein:
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 04 Déc 2014, 11:47
par arnaud32 » 04 Déc 2014, 11:47
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités