Derivee A Deux Variables !
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
sophie_lee
- Membre Naturel
- Messages: 33
- Enregistré le: 03 Mai 2013, 16:59
-
 par sophie_lee » 03 Mai 2013, 17:01
par sophie_lee » 03 Mai 2013, 17:01
Bonjour tout le monde, j'ai rencontré un petit souci concernant des dérivées à deux variables, voiçi la question : :cry:
soit la fonction f= m/(p1+0,3p2)
il faut que je la dérive par rapport à p1, mais à plusieurs reprises, j'ai pas reussit à trouver la bonne réponse qui est :
-m/(p1+0,3p2)^2
et aussi une autre :
soit la fonction g = 0,3m/(p1+0,3p2)
il faut que je la dérive par rapport à p2, mais j'abouti pas à ce résultat : (-0,3m x 0,3 )/ (p1+0,3p2)^2
HELPPPPPPP !!!!!!!!!!!!!! :help: :help:
-
Archibald
- Membre Relatif
- Messages: 415
- Enregistré le: 05 Avr 2013, 17:06
-
 par Archibald » 03 Mai 2013, 17:22
par Archibald » 03 Mai 2013, 17:22
Bonjour,
 = \frac {\partial (m/(p_1+0,3p_2)}{\partial p_1} = \frac {m'(p_1+0,3p_2)-m(p_1+0,3p_2)'}{(p_1+0,3p_2)^2} = \frac {0-m(1+0)}{(p_1+0,3p_2)^2} = \frac {-m}{(p_1+0,3p_2)^2})
Tu as compris ? essaye de faire la seconde
-
sophie_lee
- Membre Naturel
- Messages: 33
- Enregistré le: 03 Mai 2013, 16:59
-
 par sophie_lee » 03 Mai 2013, 17:31
par sophie_lee » 03 Mai 2013, 17:31
Archibald a écrit:Bonjour,
 = \frac {\partial (m/(p_1+0,3p_2)}{\partial p_1} = \frac {m'(p_1+0,3p_2)-m(p_1+0,3p_2)'}{(p_1+0,3p_2)^2} = \frac {0-m(1+0)}{(p_1+0,3p_2)^2} = \frac {-m}{(p_1+0,3p_2)^2})
Tu as compris ? essaye de faire la seconde
Heu non, j'ai compris que c'était le forme de u'v - v'u / v^2
mais je vois pas comment le v il a disparu enfaite, je trouve : (p1+0,3p2) - m / (p1+0,3p2)^2 ..
-
Archibald
- Membre Relatif
- Messages: 415
- Enregistré le: 05 Avr 2013, 17:06
-
 par Archibald » 03 Mai 2013, 17:54
par Archibald » 03 Mai 2013, 17:54
Quelle est la dérivée de

par rapport à

?
-
sophie_lee
- Membre Naturel
- Messages: 33
- Enregistré le: 03 Mai 2013, 16:59
-
 par sophie_lee » 03 Mai 2013, 18:18
par sophie_lee » 03 Mai 2013, 18:18
Archibald a écrit:Quelle est la dérivée de

par rapport à

?
Ahh d'accord même u il faut le dérivé par rapport à p1 ! moi je voyais que v enfaite, oh lala j'ai fait tout un plat. en tout cas merci

-
Archibald
- Membre Relatif
- Messages: 415
- Enregistré le: 05 Avr 2013, 17:06
-
 par Archibald » 03 Mai 2013, 18:32
par Archibald » 03 Mai 2013, 18:32
Pourtant, tu l'as écrit par toi-même plus-haut ;) (cf. "j'ai compris que c'était le forme de u'v - v'u / v^2 "
avec u = m d'où u' = 0 et u'v produit nul.)
Je t'en prie, ce fut un plaisir. ;)
-
sophie_lee
- Membre Naturel
- Messages: 33
- Enregistré le: 03 Mai 2013, 16:59
-
 par sophie_lee » 03 Mai 2013, 18:39
par sophie_lee » 03 Mai 2013, 18:39
Archibald a écrit:Pourtant, tu l'as écrit par toi-même plus-haut

(cf. "j'ai compris que c'était le forme de u'v - v'u / v^2 "
avec u = m d'où u' = 0 et u'v produit nul.)
Je t'en prie, ce fut un plaisir.

m' = 1 non ? c'est comme x' = 1.
mais vu que là dans u il n'y a pas de p1, donc c'est 0 c'est pas comme ça qu'il faut résonner ?
-
Archibald
- Membre Relatif
- Messages: 415
- Enregistré le: 05 Avr 2013, 17:06
-
 par Archibald » 03 Mai 2013, 18:48
par Archibald » 03 Mai 2013, 18:48
Oui, c'est ça. Quand on dérive par rapport à une variable

, les autres variables sont considérées comme des constantes. Or la dérivée d'une constante seule est nulle, d'où
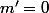
En ravanche,
')
aurait donné

car
'=k)
-
sophie_lee
- Membre Naturel
- Messages: 33
- Enregistré le: 03 Mai 2013, 16:59
-
 par sophie_lee » 03 Mai 2013, 19:05
par sophie_lee » 03 Mai 2013, 19:05
Archibald a écrit:Oui, c'est ça. Quand on dérive par rapport à une variable

, les autres variables sont considérées comme des constantes. Or la dérivée d'une constante seule est nulle, d'où
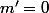
En ravanche,
')
aurait donné

car
'=k)
d'accord, j'ai bien compris. Merci :id:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
(cf. "j'ai compris que c'était le forme de u'v - v'u / v^2 "
