Dérivée de la composée de deux applications

[legeniedesalpages]

Bonsoir, il y a quelques points de cette démonstration que j'ai du mal à comprendre:

Théorème:

Soient , et trois espaces vectoriels réels de dimension finie.
Soit une application à valeurs dans définie sur la partie ouverte de .
Soit une fonction à valeurs dans définie sur une partie ouverte de contenant .
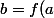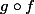
Alors si est dérivable en et est dérivable en alors est définie sur à valeurs dans et dérivable en .
De plus




démonstration:

Etant donné il s'agit de montrer que la norme de



vérifie

.

Pour tenir compte du fait que et sont dérivables on pose avec

;



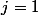
et l'on est ramené à montrer que pour et

.

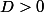
Or il existe tel que pour tout dans .
Et comme est dérivable en , il existe tel que pour .

Et ces deux inégalités montrent pour .

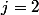
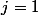
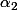
Pour traiter le cas , on note d'abord qu'il existe et tels que entraîne .
D'autre part, comme est dérivable en on a



à condition que soit assez petit, ce qu'on réalise en prenant assez petit.

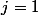
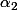
Donc on réalise pour et en prenant assez petit puis .



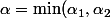Déjà je ne comprends pas trop quel genre d'éléments est C(x).

L'auteur voulait-il dire:


ou



ou encore autre chose ?

Merci pour vos indications

[Joker62]

Bé y'a beaucoup plus simple pour montrer que (gof)'(a) = g'(f(a)).f'(a)
Enfin, simple, y'a juste beaucoup de calcul et de mise en forme.

Tu tiens absolument à comprendre cette démo qui me semble très tordue lol :D ???

[legeniedesalpages]

voui je tiens absolument à la comprendre lol

Bonsir au fait joker

[barbu23]

Bonsoir "legeniedesalpages" :
tu trouveras la demonstration de ton théorème, sur le lien suivant ( page 21 ) :
[url=http://]http://math1.unice.fr/~comte/L1b/CoursComplet.pdf[/url]

[legeniedesalpages]

Bonsoir "legeniedesalpages" :
tu trouveras la demonstration de ton théorème, sur le lien suivant ( page 21 ) :
[url=http://]http://math1.unice.fr/~comte/L1b/CoursComplet.pdf[/url]

barbu pourquoi tes liens renvoient toujours vers "http:/" :lol2:

[Joker62]

Désolé je dis jamais bonsoir quand je réponds lol :)

Donc Bonsoir ;), j'vais essayer de comprendre un peu ton bordel :)

Edit : Merci pour le cours Barbu ;), je n aime pas trop celui de mon prof :S
Edit Bis : C est vrai que Barbu a du mal avec ses liens lol

[legeniedesalpages]

c'est vrai que ce pdf a l'air sympa. Tu as du calcul diff ce semestre joker?

[Joker62]

Ouai, mais ça me saoule assez, parce que ça parle pour l'instant de continuïté, de Jacobienne, de dérivée partielle, choses que j'ai déjà vues au semestre 4 et donc j'aimerai bien passer à autre chose lol :)

[legeniedesalpages]

ah oui je comprends. J'en avais fait au semestre 3 mais je ne comprenais pas grand chose. Apparemment on va en refaire au semestre 6, mais de façon plus approfondi, j'imagine qu'on aura des rappels de ce genre aussi, ce qui ne me fera pas de mal :langue:

[Joker62]

Moi au semestre 6, c'est plus du calcul diff, c'est du calcul intégrale :p
Hum ça sent bon, Mesure de Lebesgues et tout plein de truc que j'vais détester lol.

[legeniedesalpages]

ah d'accord, c'est l'inverse de moi.
Enfin je trouve que l'intégrale de Lebesgue est plutôt sympa, avec la théorie de la mesure.

[legeniedesalpages]

ok, je crois que je commence à comprendre pour le C(x),

on veut donc montrer qu'il existe une application linéaire L de E dans G telle que

,

et que ,

autrement dit que ,

ceci équivaut aussi à dire que

pour tout , il existe avec et entraîne que



Si je pose , cela revient donc à dire que

pour tout , il existe avec et entraîne que



Donc en fait je crois que C(x) désigne .

ok donc C(x) est dans G.

[legeniedesalpages]

par contre, je ne vois pas pourquoi ??

[legeniedesalpages]

Ah je crois qu'en fait, l'auteur voulait plutôt dire:

,

du coup c'est bon pour la somme.

[legeniedesalpages]

Je ne comprends pas comment on peut affirmer qu'il existe tel que pour tout dans ???

[legeniedesalpages]

C'est bon, en fait je ne me rappelais plus qu'en définition finie toute application linéaire L est continue et qu'il existe tel que
[CENTER] pour tout x dans E.[/CENTER]