Dérivé d'une intégral

[lightone]

Bonjour, j'ai un problème avec mon exo, alors le voici :

Soit f : R -> R une fonction continue et soit alpha : R -> R la fonction définie par

alpha(x) = Intégrale de sin(x-t)f(t)dt sur l'intervalle [0, x]

Montrer que alpha est solution de l'équation différentielle de alpha'' + alpha = f.


Alors moi j'ai calculé alpha' puis alpha'' mais je me retrouve bloqué. Déja, est ce que j'ai la bonne démarche?
Je vous remercie pour vos futurs réponses.

[zygomatique]

salut

oui la démarche est bonne ...

montre nous a'(x) et a"(x) ....

[lightone]

j'ai trouvé : a'= f(0)*cos(-t)+-sin(-t)*f'(0)
et pour a''= f(0)*sin(-t)+cos(-t)*f'(0)+f'(0)*cos(-t)+-sin(-t)*f''(0)

[Ben314]

Salut,
Perso, je ne trouve (pas du tout) ça.
Comme tu n'est pas en "temps limité", je te suggérerais bien de prendre au moins un (ou deux) exemples :
- Si la fonction f de départ est constante égale à 1, c'est quoi la fonction ?
Est-ce que ça "colle" avec ce que tu as trouvé concernan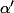t et ?
- A la limite, pour faire dans le "un peu moins trivial", tu peut regarder ce que ça donnerais si la fonction de départ est définie par ou bien (dans les deux cas, un peu de calculs, mais évidement ça semble bien plus pertinent comme exemple pour vérifier les résultats obtenus)

[lightone]

Je ne comprend pas tout ce que tu dis Ben314..... f(t) n'est pas défini, je sais juste que cette fonction est continue et qu'elle appartient à R.

[lightone]

ah oui je viens de voir que je me suis planté quelque part, je refais

[Ben314]

f(t) n'est pas défini, je sais juste que cette fonction est continue et qu'elle appartient à R.

Ben justement, pour éviter de travailler dans le "pure abstrait" et pour pouvoir vérifier tes résultat, je te suggère de prendre un ou deux exemples de fonction f.
Ça ne permet évidement pas de répondre à la question concernant le cas général, mais ça évite au moins d'écrire des grosse conneries vu que, si ton truc ne marche pas avec un exemple (simple) de fonction f, tu est sûr et certain qu'il est faux.

C'est très exactement la même chose que, face à un collégien qui me demande si c'est vrai ou pas que, pour tout réel A et B on a (A+B)²=A²+B², il me semble que le moins con à lui répondre, c'est "ça donne quoi ton truc sur l'exemple A=2 , B=3 ?"

[lightone]

Oui mais tu m'as dit que tu ne trouves pas ça donc j'ai pas besoin de vérifier ce que j'ai puisque je n'aurais pas d'égalité. Mais je ne vois pas ou je me suis trompé.

[Ben314]

Comment procède tu ?


P.S. : même si, jusque là, ma parole te suffit pour être persuadé que ton résultat est faux (pourvu que ça dure...), ça peut être pas con de regarder un exemple pour vérifier la suite de l'exo. Mais c'est vrai que ça peut attendre...

[lightone]

Ba si je me retrouve bloqué, c'est que ce n'est pas ça....

Alors moi j'ai fait ça [sin(x-t)f(t)] avec 0 et x en indice, puis j'ai du coup on a : [sin(x-x)f(x)]-[sin(x-0)f(0)] et du coup j'ai -[sin(x)f(0)] après j'ai fait la dérivé donc dérivé de -sin(x)est -cos(x) et celui de f(0)est f'(0) et donc la dérivé de tout ça est -sin(x)*f'(0)+f(0)*(-cos(x)). Déja là ou est la faute?

[Pythales]

Avant tout, peux-tu nous dire quelle est la dérivée de ?

[lightone]

Aucune idée, je ne suis pas un expert en dérivé, on a eu le cours que cette semaines et ça ne traite pas directement de ça

[Ben314]

Ce que tu fait, ça semble assez nettement être "n'importe quoi".
As tu dans ton cours la réponse à la question posée par Pythales ?
Elle peut éventuellement ne pas y être (ça dépend du cursus que tu suis), auquel cas il faut passer par la notion de fonctions de plusieurs variables et de dérivées partielles.
Évidement ça demande à avoir vu ces notions : est-ce le cas ?

Si tu n'a ni l'un ni l'autre, ben... je sais pas comment tu es sensé faire...

[lightone]

Dans mon cours, j'ai le théorème fondamental de l'analyse et sa démonstration, et juste 3 coro avec aussi leur démonstration, c'est tout. Je ne peux pas répondre à la question de pythales car je n'ai pas fait ça en cours.

[lightone]

Je suis en L1 et on vient de commencer la partie dérivabilité avec les intégrales.

[Kolis]

Bonjour !
Ne serait-ce pas plus simple de développer ce qui ne demande ensuite que de dériver des fonctions ?

[Ben314]

Si tu n'a ni l'un ni l'autre, ben... je sais pas comment tu es sensé faire...

Ne serait-ce pas plus simple de développer ce qui ne demande ensuite que de dériver des fonctions ?

Maintenant je sais...
Enfin bref, tu t'empresses de faire ce que dit Kolis et tu oublie le reste...

Comme quoi, quand on connait les "gros outils" adaptés au problème, on a du mal à voir les trucs "élémentaires"...

[lightone]

ok je vais voir ça plus tard, je vous tiendrais au courant.

[lightone]

petite question, vous me dites de dériver. Mais avant, je ne dois pas plutot donner la primitive de sin(x-1)f(t) pour avoir une expression égale à l'intégrale puis ensuite dérivé?

[Ben314]

Je ne pense pas que ce soit judicieux à ton niveau vu qu'il faudrait (évidement) préciser de quelle primitive tu parle (il y a deux variables x et t dans le bidule donc on peut "primitiver" "en x" ou "en t") et donc faire assez clairement référence à des fonctions de plusieurs variables et a la notion de dérivées partielles.

Alors qu'avec la méthode de Kolis consistant uniquement à écrire différemment le truc à intégrer (et pas à le calculer) de façon à avoir des fonctions ne dépendant que de t à intégrer, on peut envisager de tout rédiger sans faire appel à la notion de fonctions de plusieurs variables.

Enfin, bref, applique à la lettre ce que Kolis a dit : tu remplace le par et ça te permet d'écrire où les 4 fonction 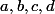sont extrêmement faciles à dériver.