Dérivation d'une fonction

par **barbu23** » 23 Fév 2015, 17:20

Bonjour à tous,

Connaissez vous une condition nécessaire et suffisante sur des fonctions réelles :

de classe

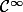
, pour que :

pour tout

?
La condition :

est toujours vérifiée, par contre la condition inverse :

, je ne sais pas sous quelles conditions elle est valable.

Merci infiniment pour votre aide. :happy3:

par **Monsieur23** » 23 Fév 2015, 17:26

Aloha,

Si f(0) = g(0), ça doit fonctionner non ?

par **BiancoAngelo** » 23 Fév 2015, 17:26

Salut.

Si les dérivées sont égales, les fonctions sont égales à une constante près.

Donc il faut rajouter une condition style

pour un

.

par **Carpate** » 23 Fév 2015, 17:29

barbu23 a écrit:Bonjour à tous,

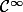
Connaissez vous une condition nécessaire ou suffisante sur des fonctions réelles : de classe , pour que :
pour tout ?
La condition : est toujours vérifiée, par contre la condition inverse : , je ne sais pas sous quelles conditions elle est valable.

Merci infiniment pour votre aide. :happy3:

Pour que f(x) =g(x), il suffit qu'il existe une valeur

telle que

par **barbu23** » 23 Fév 2015, 17:32

Merci beaucoup Monsieur23, BiancoAngelo et Carpate pour ces précisions. :we:
Donc, si le graphe des deux fonctions

et

se croisent en un point, alors forcément, la proposition est valide.

par **Doraki** » 23 Fév 2015, 18:59

J'ai pas compris si f est définie sur R ou sur Df.

Dérivation d'une fonction

Dérivation d'une fonction

Qui est en ligne